SUMMARY
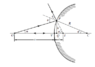
The discussion focuses on the derivation of angle relationships in geometrical optics involving spherical mirrors. Specifically, it examines the equations θ = φ + α and 2θ = α + α', questioning the application of the exterior angle theorem for triangles in their formulation. The participants confirm that both equations stem from the same theorem, highlighting the geometric principles at play in light ray interactions with spherical mirrors.
PREREQUISITES
- Understanding of geometrical optics principles
- Familiarity with the exterior angle theorem for triangles
- Knowledge of spherical mirror properties
- Basic trigonometry related to angles
NEXT STEPS
- Study the derivation of angle relationships in spherical mirrors
- Learn about the application of the exterior angle theorem in optics
- Explore the properties of light reflection on curved surfaces
- Investigate advanced geometrical optics concepts, such as ray tracing
USEFUL FOR
Students of physics, optics enthusiasts, and educators looking to deepen their understanding of light behavior on spherical mirrors.