Geometry proof Mid point theorem

[mathlearn]

Hi,I have been stuck on this problem

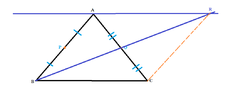
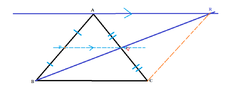
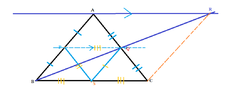
The midpoints of the sides AB and AC of the triangle ABC are P and Q respectively. BQ produced
and the straight line through A drawn parallel to PQ meet at R. Draw a figure with this information
marked on it and prove that, area of ABCR = 8 x area of APQ.

I drew a figure with all the information included,

View attachment 5790

and I am having trouble saying that ABCR = 8 x area of APQ. & I think it has got something to do with The Midpoint theorem.Try your best to explain your answer

Many thanks:)

 

[Evgeny.Makarov]

and I am having trouble saying that ABCR = 8 x area of APQ.

You just said it! (Smile)

If we denote the middle of $BC$ by $S$, it is easy to prove that segments $PQ$, $PS$ and $QS$ divide $\triangle ABC$ is into four equal (i.e., congruent) triangles. Thus, the area of $\triangle APQ$ is $1/4$ of the area of $\triangle ABC$. Another fact that is needed is that $\triangle ABC=\triangle ARC$.

 

[mathlearn]

Many Thanks,
I see that the $$\triangle APQ \equiv \triangle PBS \equiv \triangle APQ \equiv \triangle QSC $$ triangles are congruent to each other by (SSS)

and I updated my picture

View attachment 5791

Can you help me to say that $$\triangle ABC=\triangle ARC$$ and to continue the proof.

I Think there are two ways of accomplishing it but not sure of them. The first one would be , ABCR is a parallelogram and $$\triangle ABC = \frac{1}{2} ABRC$$

and the other way not sure whether it's correct; it would be to say BQ=QR somehow.

Can you help me to proceed.

Many Thanks :)

 

[Evgeny.Makarov]

Can you help me to say that $$\triangle ABC=\triangle ARC$$ and to continue the proof.

This should say, "Can you help me prove that $$\triangle ABC=\triangle ARC$$..."

I Think there are two ways of accomplishing it but not sure of them. The first one would be , ABCR is a parallelogram and $$\triangle ABC = \frac{1}{2} ABRC$$

ABCR is definitely a parallelogram, the question is just how to show it. It may depend on the facts that have already been proved in your course.

It is not good to say $$\triangle ABC = \frac{1}{2} ABRC$$ because the operation of multiplying a quadrangle by a number is not defined.

and the other way not sure whether it's correct; it would be to say BQ=QR somehow.

This is also true, but requires a proof.

One way is to note that $\angle BCA=\angle CAR$ as alternate angles at parallel lines and $\angle BQC=\angle RQA$ as vertical angles. Therefore, $\triangle AQR=\triangle CQB$ by ASA (the equal sides are $AQ$ and $CQ$). In particular, $AR=BC$. Then $\triangle ABC=\triangle CRA$ by SAS (the equal angles are $\angle BCA$ and $\angle CAR$).

 

[mathlearn]

Many Thanks :) for your clear explanation,

So now $$\triangle ABC \equiv \triangle CRA$$ Under (SAS);

Now it is obvious that ABCR = 8 x area of APQ;

How should I say that ,

Can you help me to proceed.

Many Thanks :)

 

[Evgeny.Makarov]

Now it is obvious that ABCR = 8 x area of APQ;

How should I say that

You just said that. It would be more correct to say that the area of $ABCR$ is 8 times the area of $APQ$.

I am not sure what you need help with.

 

[mathlearn]

Many Thanks :)

Now I think the problem should ended by finally writing "ABCR = 8 x area of $$\triangle$$PQR " after saying $$\triangle ABC≡ \triangle CRA under (SAS)$$ & thanks for your very clear explanation on the problem.

Many Thanks:)

 

[Evgeny.Makarov]

Now I think the problem should ended by finally writing "ABCR = 8 x area of $$\triangle$$PQR "

Once again, the area of $ABCR$. A quadrangle can't equal a number.

 

[mathlearn]

Hi,

$$ \therefore area of ABCR = 8 times the area of \triangle PQR $$

So that's It problem solved.

Many Thanks for your detailed and clear explanations (Smile);

 

[raj2sherma]

Proof :
ABCR = 2ABR∆ (Diagonal bisect the area of a parallelogram)
ABR∆ = 2ABQ∆ ( Base BQ is half from BR and height is same for both triangles)
ABQ = 2APQ∆ ( Base AP is half from AB and height is same for both triangles)
∴ ABCR = 2ABR∆ = 2 * 2ABQ∆
ABCR = 4ABQ∆ = 4 * 2APQ∆
ABCR = 8APQ∆