It's basically the same as what you've got. My point was that it wasn't evident how you got those numbers. (I get approx. 19.07 with your equation too, if I don't round off the intermediate steps).
So here's my solution, with justifications:
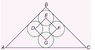
Like you said, we have \angle B = 90^\circ[/tex] and, with \triangle ABC[/tex] being isosceles, we have \angle A = \angle C = 45^\circ[/tex] and \scriptstyle \overline{AB} \, = \, \overline{BC}<br />
<br />
Drawing the height of \triangle ABC[/tex] from B perpendicular to \scriptstyle \overline{AC} intersecting at point H (the tangent point with circle G), we will have a line segment that bisects circles E and G through their centers. Therefore, the height of \triangle ABC[/tex] is equal to the length of the diagonal of square DEFG (which is \scriptstyle \overline{EG}) plus the radius of circle G (which is \scriptstyle \overline{GH}) plus the length of \scriptstyle \overline{BE} (which can be shown to be equal to half the length of \scriptstyle \overline{EG}).<br />
<br />
Being an isosceles triangle, this height \scriptstyle \overline{BH} will bisect \angle B[/tex], forming a new isosceles triangle \triangle ABH[/tex] having \scriptstyle \overline{AH} \, = \, \overline{BH}<br />
<br />
But (like you stated), we have the area of<br />
<br />
\triangle ABC = \frac{1}{2} \overline{AB} \times \overline{BC} = \frac{1}{2} \overline{AB}^2 = 10,000<br />
<br />
<br />
This gives us<br />
<br />
\overline{AB} = \sqrt{20,000} = 100 \sqrt2 \approx 141.4<br />
<br />
<br />
But this is the hypotenuse of \triangle ABH[/tex], so we have \scriptstyle \overline{AH} \displaystyle ^2 +~ \scriptstyle \overline{BH} \displaystyle ^2 = 2 \times\scriptstyle \overline{BH} \displaystyle ^2 = 20,000 and \scriptstyle \overline{BH} \displaystyle= 100<br />
<br />
Call R the radius of the circles. Then you get the length of a side of square DEFG equal to 2R and it's diagnonal (say, \scriptstyle \overline{EG} equal to \sqrt{(8R^2)} = 2R \sqrt(2)[/tex]<br />
<br />
<br />
So,<br />
<br />
\overline{EG} = 2R \sqrt2<br />
<br />
\overline{BE} = \textstyle \frac{1}{2} \displaystyle \overline{EG} = R \sqrt2<br />
<br />
\overline{GH} = R<br />
<br />
<br />
Therefore,<br />
<br />
\overline{BH} = 2R \sqrt2 ~+~ R \sqrt2 ~+~ R = 3R \sqrt2 ~+~ R = \overline{AH} = 100<br />
<br />
<br />
Solving for R,<br />
<br />
R \times \left( 3 \sqrt2 \, + 1 \right) = 100<br />
<br />
R = \frac{100}{3 \sqrt2 \, + 1} \approx 19.07