- #1
RGann
- 12
- 1
A seemingly good way to understand the overshoot and decay (ringing) of a square wave on a scope is that it is the result of bandwidth limiting. In that case, the Fourier series of a square wave
[tex]\Pi(t) = \frac{1}{2 \pi} \sum_{n=-\infty}^\infty \frac{\sin(n \omega/2)}{n \omega/2} \exp(i n \omega t)[/tex]
shows the well-known overshoot when n is only taken to a small number, such as 30, terms.
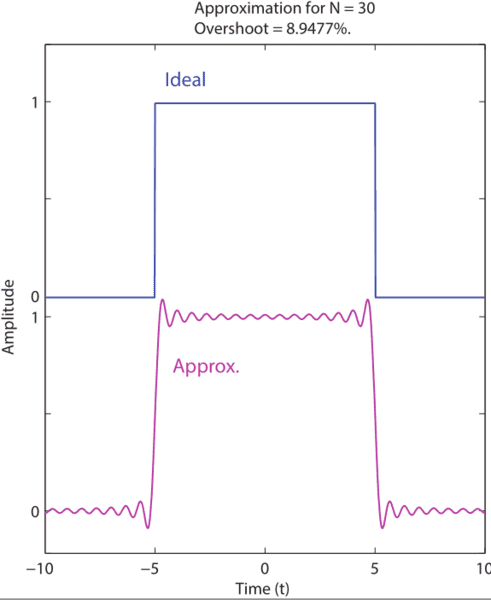
It's obtained by Fourier transforming the rect function [itex]\Pi(t)[/itex] to get [itex]\mathrm{sinc}(\omega)[/itex], then transforming back to the time domain, except you form a Riemann sum instead of an integral and take finite terms.
But this calculation doesn't reproduce what you really see on a scope, because it appears to be non-causal. That is, before the machine that drives the signal starts to apply voltage (at [itex]t=-5[/itex] in the plot), this curve is already ringing. There's a few references to the causality being related to the Kramer's-Kronig relations, especially in the "Understanding the Kramers-Kronig Relation Using A Pictorial Proof" white paper availble online (here). In that they suggest forming a causal function, where it is zero for all [itex]t < 0[/itex], which we could do by translating the rectangle function so that its rise is at [itex]t=0[/itex]. Then form even and odd functions out of the signal. When you do this, the odd function is the same as the even function times [itex]\mathrm{sgn}[/itex]. However, this seems to be of little help, particularly because finding the Fourier transform of the odd part
[tex] h_o = \mathrm{sgn}(t) h_e = (1/2) \mathrm{sgn}(t) \Pi(t) [/tex]
involves a convolution of [itex]\mathrm{sinc}[/itex] and [itex]1/i \omega[/itex], which is quite difficult (Wolfram integrator gives an answer that is not pure imaginary, which shouldn't be true).
What am I missing here? Is there a way to present the real signal you see on a scope trace as an instance of the Gibbs phenomenon? If so, is this on the right track? Does anyone know of a treatment of this problem?
Thanks!
[tex]\Pi(t) = \frac{1}{2 \pi} \sum_{n=-\infty}^\infty \frac{\sin(n \omega/2)}{n \omega/2} \exp(i n \omega t)[/tex]
shows the well-known overshoot when n is only taken to a small number, such as 30, terms.
It's obtained by Fourier transforming the rect function [itex]\Pi(t)[/itex] to get [itex]\mathrm{sinc}(\omega)[/itex], then transforming back to the time domain, except you form a Riemann sum instead of an integral and take finite terms.
But this calculation doesn't reproduce what you really see on a scope, because it appears to be non-causal. That is, before the machine that drives the signal starts to apply voltage (at [itex]t=-5[/itex] in the plot), this curve is already ringing. There's a few references to the causality being related to the Kramer's-Kronig relations, especially in the "Understanding the Kramers-Kronig Relation Using A Pictorial Proof" white paper availble online (here). In that they suggest forming a causal function, where it is zero for all [itex]t < 0[/itex], which we could do by translating the rectangle function so that its rise is at [itex]t=0[/itex]. Then form even and odd functions out of the signal. When you do this, the odd function is the same as the even function times [itex]\mathrm{sgn}[/itex]. However, this seems to be of little help, particularly because finding the Fourier transform of the odd part
[tex] h_o = \mathrm{sgn}(t) h_e = (1/2) \mathrm{sgn}(t) \Pi(t) [/tex]
involves a convolution of [itex]\mathrm{sinc}[/itex] and [itex]1/i \omega[/itex], which is quite difficult (Wolfram integrator gives an answer that is not pure imaginary, which shouldn't be true).
What am I missing here? Is there a way to present the real signal you see on a scope trace as an instance of the Gibbs phenomenon? If so, is this on the right track? Does anyone know of a treatment of this problem?
Thanks!
![ScreenClip [1].png](/data/attachments/48/48887-d79f1c242eadd5b764e1e081fd3ff9eb.jpg)
