Glider pulled by suspended mass

  • Thread starter Thread starter slapshot151
  • Start date Start date
  • Tags Tags
    Mass
AI Thread Summary
The discussion revolves around a physics problem involving a glider and a hanging mass connected by a string over a pulley. Participants are trying to derive the relationship between the speeds and accelerations of the glider and the hanging mass, specifically vx = uvy and ax = uay. There is confusion regarding the application of differentiation and the chain rule to relate the variables involved. One user expresses frustration after spending several hours on the problem and seeks clarification on the geometric relationships between the variables. The conversation highlights the importance of understanding how changes in one variable affect others in the system.
slapshot151
Messages
6
Reaction score
0

Homework Statement



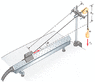
A 1.00-kg glider on a horizontal air track is pulled by a string at an angle θ . The taut
string runs over a pulley and is attached to a hanging object of mass 0.500 kg . (a) Show that the speed vx of the glider and the speed vy of the hanging object are related by vx = uvy, where u = z(z2–h02)–1/2. (b) The glider is released from rest. Show that at that instant the acceleration ax of the glider and the acceleration ay of the hanging object are related by ax = uay.


Homework Equations



vy2+h02=z2 (i think...)

The Attempt at a Solution



having problems with part b)
i tried to obtain vx=uvy by deriving the following equation by t:

vy2+h02=z2

see attachment for my attempt.

i've been working on this one problem for a few hours now... i don't get it
 

Attachments

  • p4-49.gif
    p4-49.gif
    25.6 KB · Views: 498
  • a.jpg
    a.jpg
    16.8 KB · Views: 386
Physics news on Phys.org
anybody?
 
Draw the triangle incorporating z, ho, and x. What is x in terms of the other variables?

When the hanging mass falls a given distance, what happens to the length of z? How does x change when z changes? How does a change in the length of z relate to the velocity of the falling mass?

Hint: Differentiation is required, and then an application of the chain rule.
 
Last edited by a moderator:

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'Calculation of Tensile Forces in Piston-Type Water-Lifting Devices at Elevated Locations'

Thread 'Calculation of Tensile Forces in Piston-Type Water-Lifting Devices at Elevated Locations'

Figure 1 Overall Structure Diagram Figure 2: Top view of the piston when it is cylindrical A circular opening is created at a height of 5 meters above the water surface. Inside this opening is a sleeve-type piston with a cross-sectional area of 1 square meter. The piston is pulled to the right at a constant speed. The pulling force is（Figure 2）： F = ρshg = 1000 × 1 × 5 × 10 = 50,000 N. Figure 3: Modifying the structure to incorporate a fixed internal piston When I modify the piston...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Determining what the y-intercept means in a force lab
Replies
7
Views
7K
How Does Gravity Affect Kinetic Energy in a Glider System?
Replies
3
Views
2K
Calculate Acceleration using relative distances
Replies
4
Views
2K
Velocity and Acceleration Relationship
Replies
13
Views
2K
How Does Cutting the String Affect the Motion of Air Track Gliders?
Replies
1
Views
11K
Air Track Glider and Hanging Block Dynamics
Replies
6
Views
7K
Linear Dynamics Help: friction and horizontal force
Replies
3
Views
2K
Solve Mass of Glider with Harmonic Motion Help
Replies
4
Views
13K
Solve Pulley-Mass System: m1=4.00 kg, m2=1.00 kg
Replies
2
Views
1K
How Do You Calculate Tension in a Rope Pulling Gliders?
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top