paul_harris77
- 50
- 0
Dear All
I am having trouble understanding the gradient vector of a scalar field (grad).
I understand that you can have a 2D/3D space with each point within that space having a scalar value, determined by a scalar function, creating a scalar field. The grad vector is supposed to point in the direction of the greatest change of the scalar function at a specific point in space. What I am stuck on is the direction of the gradient vector that grad gives you.
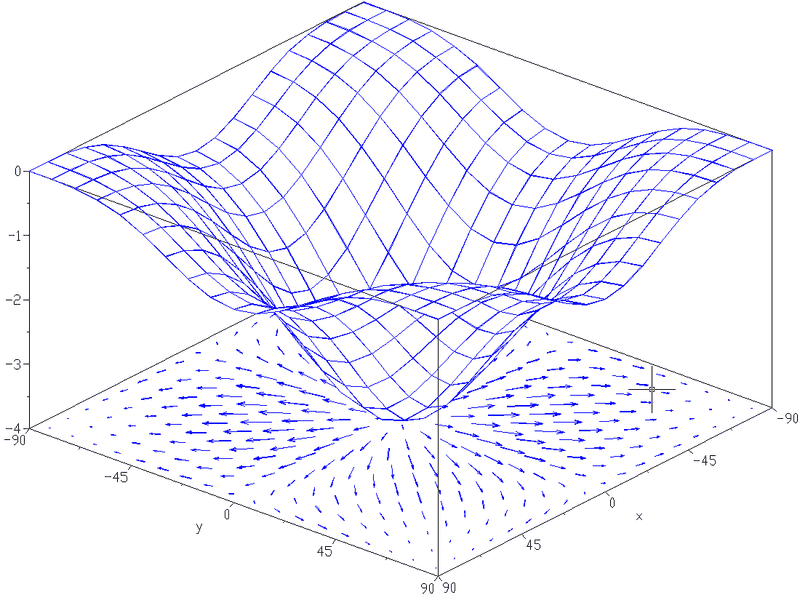
As an example, (see image below), say there is a 2D space in the x,y domain and a 2D scalar function, f(x,y). The scalar function produces a 3D surface when plotted against x and y as shown in the image below.
Text books tell you that at a specific point in space the grad vector points in the direction of the greatest change of the scalar function. But it also states that this is perpendicular to the 3d surface tangent plane at this point.
If the later point is true, then surely grad would output a 3d gradient vector, as I cannot see how it can be perpendicular to a 3d surface otherwise. However, I know the grad function is meant to output a 2d gradient vector as it uses a 2d scalar function in this case.
On the wikipedia image below, you can see that the grad vectors are in the 2D x-y plane but they are not perpendicular to the surface at that point (or else they would be pointing up or down too).
I am sure I am misinterpreting this somewhere, but I can't figure out where!
Any help would be greatly appreciated
Many thanks
Paul
I am having trouble understanding the gradient vector of a scalar field (grad).
I understand that you can have a 2D/3D space with each point within that space having a scalar value, determined by a scalar function, creating a scalar field. The grad vector is supposed to point in the direction of the greatest change of the scalar function at a specific point in space. What I am stuck on is the direction of the gradient vector that grad gives you.
As an example, (see image below), say there is a 2D space in the x,y domain and a 2D scalar function, f(x,y). The scalar function produces a 3D surface when plotted against x and y as shown in the image below.
Text books tell you that at a specific point in space the grad vector points in the direction of the greatest change of the scalar function. But it also states that this is perpendicular to the 3d surface tangent plane at this point.
If the later point is true, then surely grad would output a 3d gradient vector, as I cannot see how it can be perpendicular to a 3d surface otherwise. However, I know the grad function is meant to output a 2d gradient vector as it uses a 2d scalar function in this case.
On the wikipedia image below, you can see that the grad vectors are in the 2D x-y plane but they are not perpendicular to the surface at that point (or else they would be pointing up or down too).
I am sure I am misinterpreting this somewhere, but I can't figure out where!
Any help would be greatly appreciated
Many thanks
Paul