Graph of electric field, determine potential

[allison08]

Homework Statement

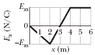
I attached a graph below.

A graph of the x component of the electric field as a function of x in a region of space is shown in Fig. 24-30. The scale of the vertical axis is set by Exs = 20.0 N/C. The y and z components of the electric field are zero in this region. If the electric potential at the origin is 19 V, (a) what is the electric potential (in V) at x = 2.0 m, (b) what is the greatest positive value of the electric potential (in V) for points on the x-axis for which 0 <= x <= 6.0 m, and (c) for what value of x is the electric potential zero?

Homework Equations

eqn1.Calculating the potential from the field:
vf=Potential final
vi=Potential initial
E = electric field
ds = an alloted distance

vf-vi = -(integral from initial to final) E dot ds

eqn2.Calculating the field from the potential:
E(sub)s = -delta V / delta S

The Attempt at a Solution

For part A I first used eqn 2 to get -20N/c = - [ (vf-19) / 2] which leads to 21 Vf, but that answer was incorrect when i submitted it.

For part C i thought at x=3, it was incorrect, then x=2 and x=4 were incorrect.
I don't know what to do for that one.

 

[collinsmark]

Hello allison08,

Welcome to Physics Forums!

For part A I first used eqn 2 to get -20N/c = - [ (vf-19) / 2] which leads to 21 Vf, but that answer was incorrect when i submitted it.

No, you can't use your second equation. That equation, E_s = -ΔV/Δs only applies for a uniform electric field. It's obvious from your attached diagram that the electric field is not uniform.

You'll have to use your

$$V_f - V_i = - \int_P \vec E \cdot \vec{ds}$$

equation.

For part C i thought at x=3, it was incorrect, then x=2 and x=4 were incorrect.
I don't know what to do for that one.

Don't just guess!

You'll have to use your integral equation.

But here's a hint: Speaking in general terms, what is the integral of a function?

Spoiler

The area under the curve.

[Edit: In other words, it is possible to complete this entire problem without doing any calculus.]

 

[allison08]

I figured the first two parts using the area under the curve!
:D