Graphing 3D Parametric Equations on Nspire: Did I Do It Right?

[ineedhelpnow]

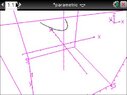
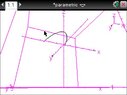
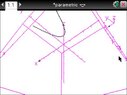
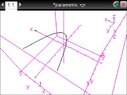
i graphed the parametric equations x=t y=t^2 and z=2 on my nspire in 3d and it came out looking like this

View attachment 3196View attachment 3195View attachment 3194View attachment 3197

(Blush) i have made them pretty so you can see the graph properly

anyways what my question is, is that ( "is is" ) is the graph supposed to look like that? on a 3d plane? did i do it right?

 

[MarkFL]

Yes, you would have the graph of $y=x^2$ on a plane parallel to the $xy$-plane, and 2 units above it. :D

 

[ineedhelpnow]

oh so its right?

honestly for a 3d graph...i thought it would have more to it, you know? i thought it would be 3d... with a hollow inside and everything...

 

[MarkFL]

oh so its right?

honestly for a 3d graph...i thought it would have more to it, you know? i thought it would be 3d... with a hollow inside and everything...

Sometimes you get curves in 3-space, sometimes you get surfaces. :D

 

[ineedhelpnow]

shouldnt it be like a flat 3d surface though?

 

[ineedhelpnow]

how is y=x^2 though. shouldn't it be x=y^2

 

[Dethrone]

Given: $x=t$, $y=t^2$

$x^2=t^2$ and $y=t^2$

Therefore, $$y=x^2$$

 

[Ackbach]

Hint: if you have one independent variable, it'll be a path or curve in space. If you have two independent variables, it'll be a surface.