Gravitational Forces and Motion in a System of Four Bodies

[whiteway]

Homework Statement

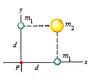
Three uniform spheres are fixed at the positions shown in the figure below. (m1 = 1.0 kg, m2 = 2.0 kg, and d = 0.60 m.)

(See attached picture)

(a) What are the magnitude and direction of the force on a 0.0250-kg particle placed at P?


(b)If the spheres are in deep outer space and a 0.0250-kg particle is released from rest 300 m from the origin along a line 45° below the -x-axis, what will the particle's speed be when it reaches the origin?

Homework Equations

I used some good old trig and GMm/r^2 to get the answers to a, which were 1.11875e-11 N and 45 degrees.

for b I really have no idea where to go with it...

The Attempt at a Solution

 

[Doc Al]

for b I really have no idea where to go with it...

Hint: What's conserved?

 

[whiteway]

hmm...
Do I need to break the problem into vector forces with GMm/r from p to each mass and find the total force by adding those?

 

[Doc Al]

hmm...
Do I need to break the problem into vector forces with GMm/r from p to each mass and find the total force by adding those?

For b you need to find the speed of the particle after it moves from its initial position (how far is that position from each mass?) to its final position at point P. Hint: Calculate the change in gravitational potential energy as it moves.