Ron777
- 2
- 0
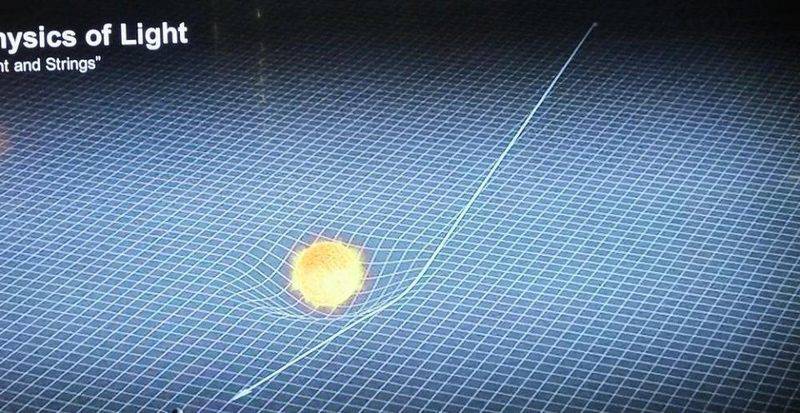
Question: If gravity can bend light toward it's source, or even hold it back so to speak (like a black hole), how does light bend around a star like photo attached? It seems if gravity pulls light toward it, the light shouldn't move out and around the star/sun but bend into it?