(h,k) of circle given D from parabola

[fedaykin]

I'm studying up for calculus I this fall, and I found a problem I can't solve.

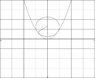
The figure (shown in attachment) shows a circle with radius 1 inscribed in the parabola y=x^2. Find the center of the circle.

So far, I have no idea. I could use the derivative to find a tangent line, then set the two distances equal to each other and solve for y, but I have no idea at what point the circle is tanget, or even if it is (at least with an analytic proof). Since I don't have the circles equation, I can't solve for points common to both equations.

 

[Defennder]

The equation of the circle is $$x^2 + (y-y_0)^2 = 1$$. You can see that the centre of the circle is on the y-axis, meaning to say it's x-coordinate is zero y0 is the y-coordinate of the centre.

Where y=x^2 and the circle intersect, the gradient of the tangent line passing through the points of intersection are the same. dy/dx for both the parabola and the circle through these points are the same for some values of y1,x1. You also know that you to find where the curve and the circle intersect, you only need relate the equation of the circle with that of the parabola.

 

[fedaykin]

When you mention gradient, I hope you're not referring to that vector field stuff referred to by the link. It will quite some time before I'm capable of understanding that.

Oy, nevermind, I'll read up on implicit derivation. It took me a while to understand that.
Thank you very very much.

 

[Defennder]

No, that has nothing to do with grad. Gradient here just refers to dy/dx. And, yeah, while implicit differentiation is not necessary, it does help a lot here.