Hamiltonian of spin 1/2 in tangential magnetic field

[johnsmi]

Hi,
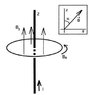
I have this article in which I saw that for a spin 1/2 particle confined to move along a ring positiond in a magnetic field with a z and \varphi

The Hamiltonian is given by: (in second attacment)
What I do not understand is how do you get the last term in the Hamiltonian.

Any help?

Thanks in advance

 

[xepma]

It comes from the standard spin-orbit coupling between the particle's magnetic moment, usually written as $$-\mathbf{\mu}_0\cdot \mathbf{B}$$. You can find a treatment on this in any book on quantum mechanics. Here, $$\mathbf{\mu}_0$$ is the magnetic moment of the spin-1/2 particle (not equal to the $$\mu$$ used in your text)

Now, to obtain the form they use you use the fact that you are dealing with spin-1/2. In that case the magnetic moment $$\mathbf{\mu}_0$$ can be written as $$-\mu \mathbf{S}/\hbar$$, where $$\mu$$ is, again, called the magnetic moment (confusing!). Furthermore, $$\mathbf{S}$$ is the spin operator which for spin-1/2 particles can be represented by the pauli matrices:

$$\mathbf{S} = (S_x,S_y,S_z) = \frac{\hbar}{2}(\sigma_x,\sigma_y,\sigma_z)$$

Plugging this into the spin-orbit coupling reproduces the term from the article, up to some constants. But you can absorb these all into the prefactor by redefining $$\mu$$ (since this is just some numerical value anyway). Hope this helps!

 

[johnsmi]

Thank you for your reply. By the way it was mentioned in the article that h bar was taken to be 1