Hamiltonian of spin 1/2 in tangential magnetic field

[johnsmi]

Hi,
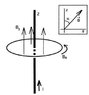
I have this article in which I saw that for a spin 1/2 particle confined to move along a ring positiond in a magnetic field with a z and \varphi

The Hamiltonian is given by: (in second attacment)
What I do not understand is how do you get the last term in the Hamiltonian.

Any help?

Thanks in advance

 

[xepma]

It comes from the standard spin-orbit coupling between the particle's magnetic moment, usually written as -\mathbf{\mu}_0\cdot \mathbf{B}. You can find a treatment on this in any book on quantum mechanics. Here, \mathbf{\mu}_0 is the magnetic moment of the spin-1/2 particle (not equal to the \mu used in your text)

Now, to obtain the form they use you use the fact that you are dealing with spin-1/2. In that case the magnetic moment \mathbf{\mu}_0 can be written as -\mu \mathbf{S}/\hbar, where \mu is, again, called the magnetic moment (confusing!). Furthermore, \mathbf{S} is the spin operator which for spin-1/2 particles can be represented by the pauli matrices:

\mathbf{S} = (S_x,S_y,S_z) = \frac{\hbar}{2}(\sigma_x,\sigma_y,\sigma_z)

Plugging this into the spin-orbit coupling reproduces the term from the article, up to some constants. But you can absorb these all into the prefactor by redefining \mu (since this is just some numerical value anyway). Hope this helps!

 

[johnsmi]

Thank you for your reply. By the way it was mentioned in the article that h bar was taken to be 1