Harmonics and oscillating atoms

[PH7SICS]

I have a question which I would like to know the answer to, I posted it before but don't think I was understood correctly, hopefully I can make myself clearer this time.

Every physical object in this universe has a natural or resonant frequency from an atom to a planet.

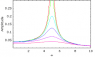
Attached is an image of a graph showing the increase in amplitude of oscillation as you approach resonance.

As you can see the system has a natural resonant frequency of 5.

Lets suppose the nucleus of an atom has a natural resonant frequency of 300hz, obviously being very small it would be much higher however let's just say its 300hz.

If we bombarded that atom with a frequency of 300hz it would go into resonance. If we were to then increase the bombarding frequency in harmonic steps of 400hz, 500hz and 600hz the nucleus would still absorb these frequency's as they are harmonics of its natural frequency however the amplitude would decrease. What I want to know is what would be the percentage of decrease in amplitude at each step. Let's assume that the amplitude of the bombarding wave is always the same and only the frequency changes. Also the bombarding wave is electromagnetic in nature not sound

 

[Bill_K]

Every physical object in this universe has a natural or resonant frequency from an atom to a planet.

No, this is not the case, for several reasons. While some things have simple, clear modes of oscillation, like a bell or a quartz crystal, other things do not. Often, the oscillations are just absorbed. Even when they are not absorbed, there is usually not just "a" natural frequency, but many. This is the reason why it is difficult to cast a bell of a shape that produces a clear tone rather than just going 'clunk'.

The nature of the oscillations can be quite different, too, depending for example on the frequency range and the nature of the driving force (mechanical, electromagnetic, etc). What is the natural frequency of a pail of water? Is it related to the sloshing of the bucket as a whole, or is it ripples in the surface, or is it sound waves propagating through the liquid.

Atoms and nuclei can absorb energy of certain frequencies, which raises them to an excited state, but this does not make them oscillate. Atoms do not oscillate. And their energy levels are not just multiples of the same frequency. Some excited states of nuclei can be understood as collective oscillation, but most are single-particle excitations.

If we bombarded that atom with a frequency of 300hz it would go into resonance. If we were to then increase the bombarding frequency in harmonic steps of 400hz, 500hz and 600hz the nucleus would still absorb these frequency's as they are harmonics of its natural frequency however the amplitude would decrease.

Harmonic frequencies are integer multiples of the fundamental frequency, so in your example the harmonics would be 600 Hz, 900 Hz, etc. There is no guarantee how a system will respond to being driven at a harmonic frequency. This is a nonlinear effect. Again, you must carefully design a bell or a violin to produce the response you want.

 

[PH7SICS]

Thanks bill_k

There are periodic tables which show that every atom (nucleus to be more precise) of every element has its own resonant frequency.

I think I am correct in saying that these nucleus will absorb energy which has a frequency matching its fundamental or natural frequency. I am aware that it will absorb energy at various frequency's as stated however there will be a frequency in which maximum absorption will be reached, I term this the resonant or natural frequency.
http://www.bruker-nmr.de/guide/eNMR/chem/NMRnuclei.html
In the example of a harmonic stretched string the harmonic are 1 (fundamental pitch) 2,3,4, 5 etc multiples.

http://en.wikipedia.org/wiki/Harmonic

 

[johng23]

He's trying to tell you that it's more complicated than you're making it out to be and then you think you can enlighten him by linking the wikipedia page to harmonics?

 

[sophiecentaur]

What sort of "natural resonance" are you referring to? There are many modes of resonance, involving a range of different forces and modes.
What is that link supposed to show?
(www.bruker-nmr.de/guide/eNMR/chem/NMRnuclei.html)
All I see is a periodic table.

I might also point out that many oscillating systems exhibit Overtones which are not actually Harmonics of a fundamental frequency. Near but by no means exact multiples of a fundamental frequency. Look up a table of quartz crystal packages and see the difference for 'overtone' specified crystals.