Heat Capacity of a Van Der Waals' gas in an Open system

[Astrocyte]

Homework Statement

Find Cp-Cv for Van Der Waals' Gas

Relevant Equations

Grand Partition Function, Grand potential.

In our class, we're using Wassermann's Thermal physics as textbook.
I always try to solve all question which included in Text book.
But sometime when I meet a problem that look like easy but actually hard, I'm so embarrassed.
This problem do also.

First, in the textbook grand potential for van der Waals' gas is

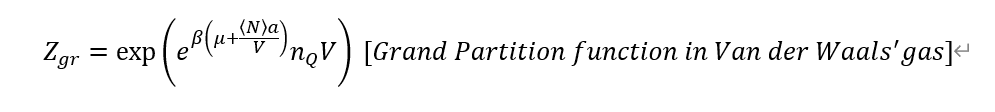
Next, I calculated routinely, but it's so complex.
The internal energy come from previous problem. I guess it's right.

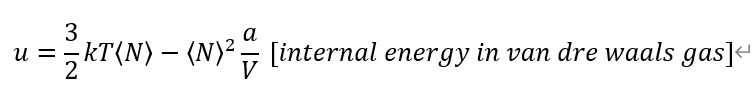
From definition of each Heat capacities. And, Entropy from Grand potential Omega.
I used previous calculation on average particle number <N>.
<N>=exp( \beta (\mu + <N>a/V))*n_Q*V
Also, n_Q is quantum concentration, which come from Ideal gas partition function, and define (m/(2*\pi*\hbar^2*\beta)^3/2
So, n_Q also depends on \beta or Temperature T.

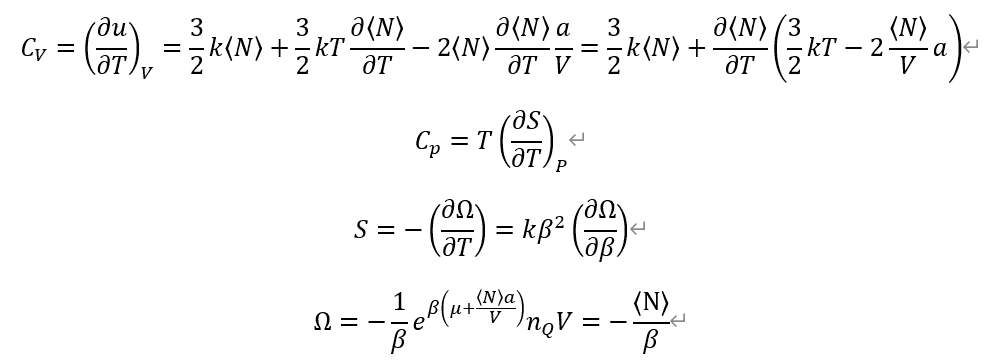
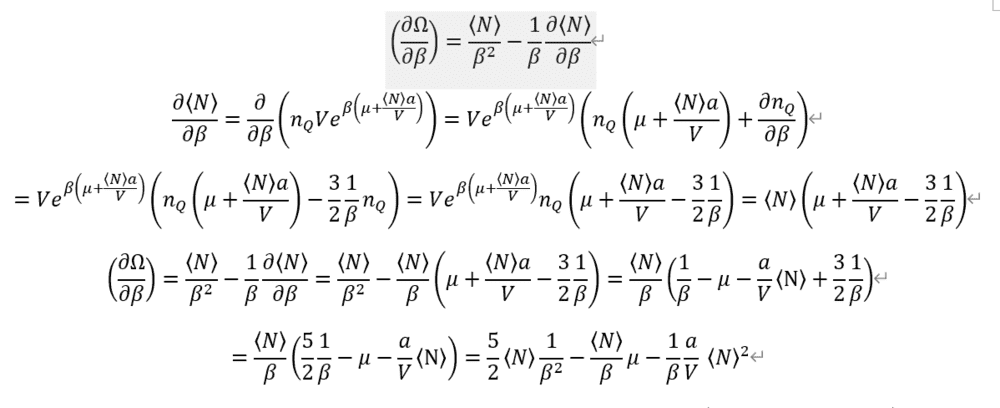
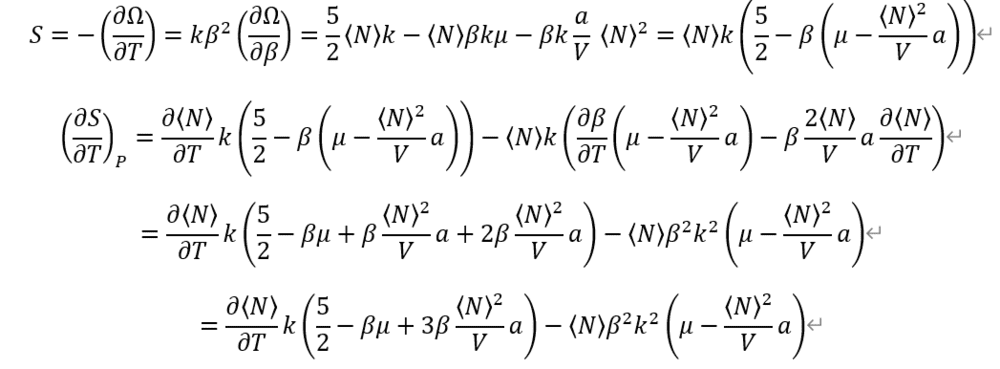
Entropy is so complex.

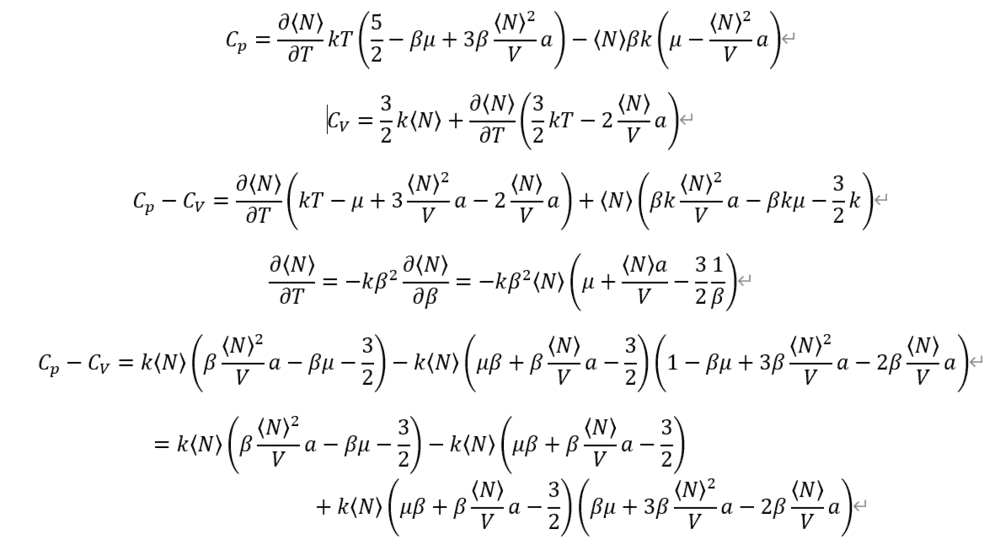
And I given up, because it's so complex for calculating by hand.
Where am I wrong?

 

[Chestermiller]

Well, one thing you're doing wrong is assuming N is a function of T.

 

[Astrocyte]

To find where i wrong, I tried to solve isobaric heat capacity in ideal gas.
So, I got entropy. it's the Sackur-Tetrode equation.
$$S=\braket{N} k[\frac{5}{2}-\beta\mu], when \;\mu \; is\; chemical\; potential.$$
it's same with
$$S=\braket{N}k[5/2-\ln{\frac{ \braket{N}}{(n_Q*V)} } ].$$
The definition of isobaric heat capacity is
$$C_{p}=T(\frac{\partial {S}}{\partial {T}})_{p},$$.
As we know, isobaric heat capacity in ideal gas is
$$C_{P}=\frac{5}{2} Nk.$$
But, I cannot prove it also...
I tried
$$C_{p}=T(\frac{\partial {S}}{\partial {T}})_{p,N}$$
It didn't work...

 

[Chestermiller]

Are you familiar with the following equation for an arbitrary equation of state:

$$C_p-C_v=T\left(\frac{\partial V}{\partial T}\right)_P\left(\frac{\partial P}{\partial T}\right)_V$$

 

[Astrocyte]

Thanks!

I have checked all of my equation... And, I found several mistakes.

By your feedback, I tried it without derivative of N respective of T.

And I got a right Cp value. 5/2 Nk.

And also I will try the equation you gave me.

Really Really Thank you. :D

 

[Chestermiller]

Thanks!

I have checked all of my equation... And, I found several mistakes.

By your feedback, I tried it without derivative of N respective of T.

And I got a right Cp value. 5/2 Nk.

And also I will try the equation you gave me.

Really Really Thank you. :D

That Cp value is only for an ideal gas, right?

 

[Astrocyte]

That Cp value is only for an ideal gas, right?

Yes. I only tried it about Cp value, because the van Der Waals gas's one is so complicated.
In addition, that Cp value come from
$$ \ln{\frac{⁡⟨N⟩}{nQV}} = \ln{\frac{⁡⟨N⟩βP}{nQ⟨N⟩}} = ln⁡{\frac{βP}{n_Q}} $$

in Entropy term.
And fortunately, In my midterm, my professor didn't ask about heat capacity, and Van der Waals' gas.