Heat in a resistor (circuit with inductor and capacitor)

[Rugile]

Homework Statement

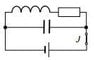
A source of ε = 10V, capacitor of C = 5 μf, inductor of L = 15 mH and r = 10 Ω and a resistor of R = 100 Ω are connected as in the schematic (attached). How much heat will dissipate in the resistor after the switch is opened?

Homework Equations

dQ = I²Rdt
KVL

The Attempt at a Solution

First of all I was quite confused by the question, so I just assumed that the switch is opened after a long time, when the capacitor and the inductor are fully charged. Then the voltage across the capacitor is U₀ = ε and the current in the inductor is I₀ = ε / (R+r). We can write the equation (KVL):
$L\frac{dI}{dt} + I(R+r) + U_C = 0$, where U_C is the voltage across the capacitor. I get stuck here - I suppose I could write second order differential equation involving the function of q: $L \frac{d^2 q}{dt^2} + (R+r) \frac{dq}{dt} + \frac{C}{q} = 0$, but I'm not sure what to do with that either. Any hints?

 

[td21]

Step 1: After switch is opened, LC oscillation occurs as described by your equation.
Step 2: Heat loss through R and r. Your task is to find out the heat loss thorugh R. At the end, all energy is dissipated through heat loss. So I suggest you find the ratio between heat loss through R: heat loss through r. I also suggest you find the initial energy.
Step 3: The ratio can be found from the ratio of R:r.

 

[Rugile]

Okay, so it is enough to find the initial energy of the system and then calculate the heat loss in R using the ratio? Can I say that the initial energy of the system (after opening the switch) was $E = \frac{CU^2}{2} + \frac{LI^2}{2}$, where $I = \frac{\epsilon}{R+r}$ and U = epsilon = EMF ?

 

[rude man]

What switch?

 

[NascentOxygen]

What switch?

The one marked with letter 'J'.

 

[Rugile]

Yes, exactly.

Does anyone have any idea if the equation of initial energy written above is correct? I have doubts about the current in the inductor, since when we open the switch it disappears (gradually), doesn't it?

 

[BvU]

O₂: Very subtle...
Rugile's post #3 seems pretty good to me: keep going !

And post #6: yes, it dampens out quickly. But the exercise only wants the total, so no need to solve the D.E.

 

[NascentOxygen]

Can I say that the initial energy of the system (after opening the switch) was $E = \frac{CU^2}{2} + \frac{LI^2}{2}$, where $I = \frac{\epsilon}{R+r}$ and U = epsilon = EMF ?

That looks right. That's the stored energy before the jumper to the battery is removed.

After the jumper is removed, the inductor current becomes the capacitor current, the two now being in series.