Qaiphyx
- 92
- 0
Helmholtz resonator equation. How do I do this?? Please help.
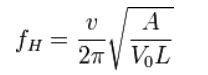
L = 0
Vo = 473.17 (I think its cubed though I calculated it from 16 ounces, so I should be cubed right??)
A = What I am solving for
F = 480 hz
V= speed of sound which is 340.19 at sea level
If Vo needs to be cubed then A should be squared, but I don't know if I am supposed to do that
Ive put all this down on paper and I am not sure how to run this equation to solve especially when it comes to the square root of a fraction, especially if the fraction is cubed and squared.
How do I do this? Been searching the internet for 2 days now trying to figure this out.
L = 0
Vo = 473.17 (I think its cubed though I calculated it from 16 ounces, so I should be cubed right??)
A = What I am solving for
F = 480 hz
V= speed of sound which is 340.19 at sea level
If Vo needs to be cubed then A should be squared, but I don't know if I am supposed to do that
Ive put all this down on paper and I am not sure how to run this equation to solve especially when it comes to the square root of a fraction, especially if the fraction is cubed and squared.
How do I do this? Been searching the internet for 2 days now trying to figure this out.