Help calculating this limit please

[Lambda96]

Homework Statement

Calculate limit of $\frac{1}{n+1} |\frac{x-1}{\xi}|^{n+1}$ as $n \rightarrow \infty$

Relevant Equations

none

Hi,

I have problems with task b, more precisely with the calculation of the limit value:

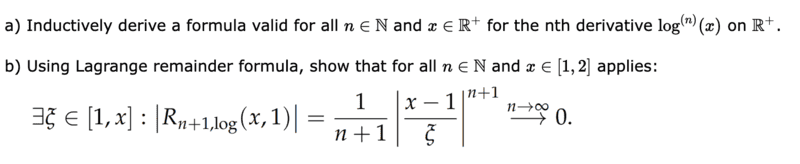
By the way, I got the following for task a $f^{(n)}(x)=(-1)^{n+1} \frac{(n-1)}{x^n}$

Unfortunately, I have no idea how to calculate the limit value for the remainder element, since $n$ appears in the exponent. I tried it with L'Hôpital's rule and then get $\Bigl( \frac{x-1}{\xi} \Bigr)^{n+1} \log(\frac{x-1}{\xi})$ and if I now form the limit, it would be $\infty$ or not?

 

[Orodruin]

Why would you apply l’Hopital? It is useful for cases when you have expressions where both numerator and denominator tend to zero.

You should focus on what is being exponentiated: $(x-1)/\xi$. What are the possible values of this?

 

[Lambda96]

Thanks Orodruin for your help , I hadn't thought of that, so the amount in the parenthesis is less than 1, which makes the limit at infinity zero.

 

[haruspex]

so the amount in the parenthesis is less than 1

Can be equal.

 

[Orodruin]

Can be equal.

Yes, but the prefactor 1/(n+1) still goes to zero so the limit is still zero. Of course, for the proof to be valid the argumentation should be the correct one though.

 

[haruspex]

but the prefactor 1/(n+1) still goes to zero so the limit is still zero

Quite so, but I was leaving that to the OP.