Help Design 4 to 16 decoder with given components

[Her-0]

I have been given the following components to design a 4 to 16 decoder:

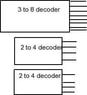
I. One 3 to 8 decoder (with enable)
II. Two 2 to 4 decoder (with enable)
III. Two NOT gates
IV. Two AND gates

I just don't understand where the AND, NOT, and enables go into. I have attached two files One with the 3 to 8 decoder, Two 2 to 4 decoder w/o the NOT gates and AND gates.

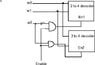
Another one of me showing how i connected TWO 2 to 4 decoders to design a 3 to 8 decoder

Can anyone help me?

 

[terranpro]

The idea is exactly the same as the 3-8 from two 2-4 case. Do you understand what you did, why you did it, and why it works?

Start by drawing a simplified truth table for a 4-16 decoder (forget about enable)

S3 S2 S1 S0 | "ON" Output
^^^^^^^^^^^^^^^^^^^^^^^^^^^
0 0 0 0 | F0
0 0 0 1 | F1
...
0 1 0 0 | F4
0 1 0 1 | F5
...
1 0 0 0 | F8
...
1 1 1 1 | F15You know that your 4-16 decoder has 16 output lines, only one line may be high for any given input scenario, and you have 3 smaller blocks to build it from. Think about partitioning off the truth table according to responsibility of each of your components.

So, your truth table has 16 possibilities - your 3-8 decoder covers 8 of those, your 2-4 decoders cover 4 each. Find the logic required to ENABLE the 3-8 decoder when it's his turn. e.g. determine which of your inputs, or their combination, allow you to drive EN high for 8 lines of your truth table above. Also remember, 3-8 decoder has 3 address lines, not 4... (what does this mean for the address lines of your 3-8 and 2-4 decoders?)

Similarly, find what logic of your inputs will enable the 2-4 decoders for ONLY the outputs you assign to them. I see two, simple solutions for the given constraints. The truth table above should really give away the answer...

- Brian