Engineering Help finding the damping ratio formula for this circuit

[Boltzman Oscillation]

Homework Statement

Derive the ordinary differential equation (ODE) for the network with the capacitor voltage vC4(t) as the dependent variable, time t as the independent variable, and Eg(t) as the network excitation described by a 10V step function. Find the resistor values that will give you a damping ratio of .1.

Relevant Equations

The damping ratio is require to be .1

The circuit to be analyzed is shown below:

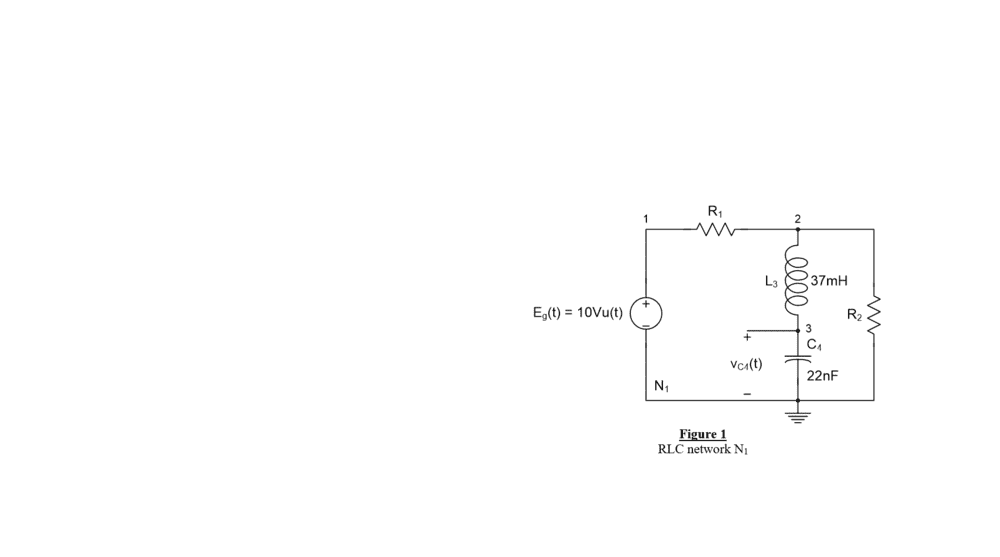
Since initial conditions are zero (from the instructions) I will use laplace transforms for the cirucit and I will use the MAME method to solve this circuit. The laplace transforms that are required will give me:
$$E_g(s) = \frac{10}{s}$$
$$ L_3 = sL_3$$
$$ C_4 = \frac{1}{sC_4}$$
again, the initial conditions are zero so i did not include them in the transforms.

Now solving the MAME (mesh analysis matrix equation), by setting the first loop as Im1 and the second loop as Im2, I get:
$$
\begin{bmatrix}
R_1+ sL_3 + \frac{1}{sC4} & -(\frac{1}{sC4} + sL_3) \\
-(\frac{1}{sC4} + sL_3) & R_2+ sL_3 + \frac{1}{sC4}
\end{bmatrix}
*
\begin{bmatrix}
I_{m1}\\
I_{m2}
\end{bmatrix}
=
\begin{bmatrix}
\frac{10}{s}\\
0
\end{bmatrix}
$$

Which is of the form:
$$Z*I = V$$
I can use Cramer's rule to solve for I_m1 and I_m2. Doing so gives me the following two formulas:

$$I_{m1} = \frac{10(R_2+ sL_3 + \frac{1}{sC4})}{s^2(L_3R_2+R_1L_3)+sR_1R_2+(\frac{R_1+R_2}{C_4})}$$

and

$$I_{m2} = \frac{10(sL_3 + \frac{1}{sC4})}{s^2(L_3R_2+R_1L_3)+sR_1R_2+(\frac{R_1+R_2}{C_4})}$$

from the circuit I can see that
$$V_{C4}(t) = \frac{I_{m1}-I_{m2}}{sC_4}$$

thus i can use my equations to solve for Vc4 as:

$$\frac{10(R_2)}{s^2(L_3R_2+R_1L_3)+sR_1R_2+(\frac{R_1+R_2}{C_4})} * \frac{1}{sC_4}$$

am i doing this right? Even if i turn this into the time domain I would have a third order differential equation in the denominator. What am I doing wrong?

 

[AVBs2Systems]

Hi BO.
the standard form of second order systems is like this:
$$
x(t) = y''(t) + 2 \delta y'(t) + \omega_{r}^{2} y(t)
$$
I would do a thevenin transform from the point of view of the branch of the inductor and capacitor in series, you get the following thevenin parameters:
$$
v_{th}(t) = E_{g}(t) \cdot \dfrac{R_{2}}{R_{1} + R_{2} }
$$

The thevenin equivalent impedence in this case:
$$
Z_{th} = \dfrac{R1 \cdot R_{2} }{R_{1} + R_{2} }
$$
Redraw the circuit, with Vth and Rth and the L and C in series, apply the standard KVL in differential equation form:
$$
V_{thevenin}(t) = V_{R thevenin}(t) + V_{L}(t) +V_{c}(t)
$$
Which becomes:
$$
V_{Th}(t) = i(t)\cdot R_{Th} + L \cdot i'(t) + \dfrac{1}{C} \displaystyle \int i(t)
$$
Remove the integral by taking the first derivative:
$$
V_{Th}'(t) = i''(t) \cdot L + i'(t) R_{Th} + \dfrac{i(t)}{C}
$$
Multiply throughout with
$$
\dfrac{1}{L}
$$
THen
$$ \dfrac{V_{Th}'(t)}{L} = i''(t) + i'(t) \dfrac{R_{Th}}{L} + \dfrac{i(t)}{LC} $$
Then the damping factor is defined as:
$$
\delta = \dfrac{R_{Th}}{2 L}
$$
And the square of the resonant angular velocity:
$$
\omega_{r}^{2} = \dfrac{1}{LC}
$$
Then the damping factor is simply:
$$
\delta = \bigg( \dfrac{R1 \cdot R2 }{R1 + R2} \bigg) \cdot \dfrac{1}{2L}
$$
The reason the damping factor is multiplied by 2 in the above equation is due to the quadratic formula:
$$
\sqrt{ 4 \cdot( \delta^{2} - \omega_{r}^{2} ) }
$$
And now you can find out the value of the thevenin resistance:
$$
R_{th} = 7.4 \,\, \text{m} \Omega
$$
What values of $$ R_{1} ,R_{2} $$ give this? My answer is to use $$ 14.8 \,\, \text{m} \Omega $$ for both. Or to decide on one value for R1 and then substitute to find the value for R2.

Original post above.