Iwanttolearnphysics
- 44
- 9
- Homework Statement
- Two boxes are sliding along a floor after being given an initial speed v to the right. The bottom box has a mass that is 4x larger than the top box. The coefficient of kinetic friction between the bottom box and the floor is μfloor. The maximum coefficient of static friction between the boxes, μbox is 0.20. Determine the maximum value of μfloor, that will allow the boxes to stop without the top box slipping with respect to the bottom box.
- Relevant Equations
- Ff = Fn x μ
Here's a picture of the question:
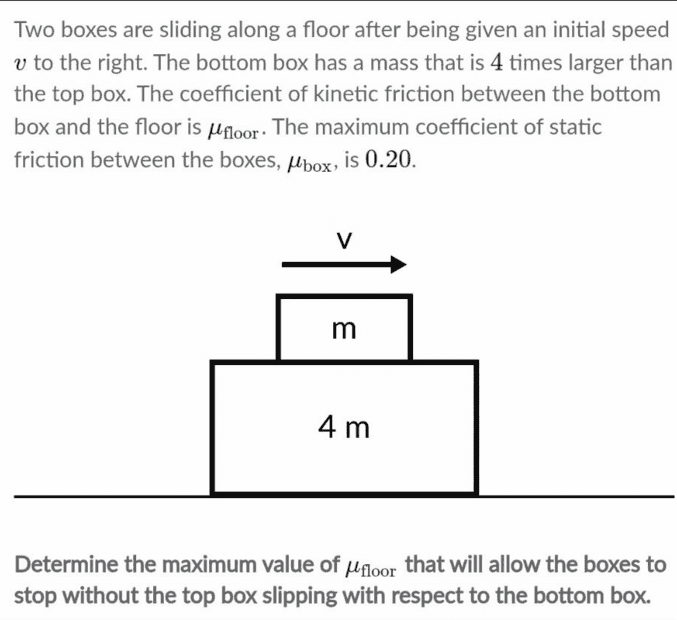
This is a Khan Academy question and although I could just click on hint to find out what the answer is, I think it would be helpful to still ask this here before looking at the answer over there, so that I know what I did wrong. Thank you in advance to anyone willing to help me.
Here's my thinking:
This is a Khan Academy question and although I could just click on hint to find out what the answer is, I think it would be helpful to still ask this here before looking at the answer over there, so that I know what I did wrong. Thank you in advance to anyone willing to help me.
Here's my thinking:
- Ff = Fn x μbox
- Ff = mg x μbox
- Ff = 1(9.81) x 0.20
- Ff = 1.96 N
- That's the friction between box m and box 4m.
- I don't know how that would help me solve the problem. It says to determine the maximum value of μfloor. How do I even relate them to each other?
- I can use Ff = Fn x μfloor
- Ff = mg x μbox
- Ff = 5(9.81) x μbox
- Now I'm stuck. I can't assume that the Friction for the floor and box m are the same as what I computed before.
- I don't know what I'm missing. It says the box was given an initial velocity, "v". But how is that helpful?