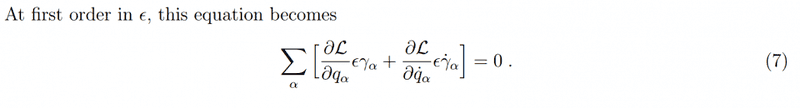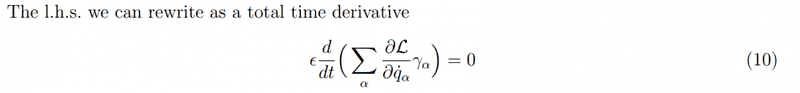Which step you don't understand? Equation (7) follows from Tylor expanding the Lagrangian:
L(x + \epsilon , y+ \eta) - L(x,y) = L(x,y) + \frac{\partial L}{\partial x} \epsilon + \frac{\partial L}{\partial y} \eta - L(x,y)
The left hand side is the variation in L, i.e., \delta L. Now take x = q, y = \dot{q}, \epsilon = \gamma and \eta = \dot{\gamma}, you get
\delta L = \frac{\partial L}{\partial q} \gamma + \frac{\partial L}{\partial \dot{q}} \dot{\gamma} .
If the transformation q^{'} = q + \gamma is a symmetry, then \delta L = 0. So, you have
\frac{\partial L}{\partial q} \gamma + \frac{\partial L}{\partial \dot{q}} \dot{\gamma} = 0.
Now, use the Lagrange equation
samalkhaiat said:
Which step you don't understand? Equation (7) follows from Tylor expanding the Lagrangian:
L(x + \epsilon , y+ \eta) - L(x,y) = L(x,y) + \frac{\partial L}{\partial x} \epsilon + \frac{\partial L}{\partial y} \eta - L(x,y)
The left hand side is the variation in L, i.e., \delta L. Now take x = q, y = \dot{q}, \epsilon = \gamma and \eta = \dot{\gamma}, you get
\delta L = \frac{\partial L}{\partial q} \gamma + \frac{\partial L}{\partial \dot{q}} \dot{\gamma} .
If the transformation q^{'} = q + \gamma is a symmetry, then \delta L = 0. So, you have
\frac{\partial L}{\partial q} \gamma + \frac{\partial L}{\partial \dot{q}} \dot{\gamma} = 0.
Now, use the Lagrange equation
\frac{\partial L}{\partial q} = \frac{d}{dt}( \frac{\partial L}{\partial \dot{q}} ) ,
in the first term and combine the two terms
\frac{d}{dt}( \frac{\partial L}{\partial \dot{q}} ) \gamma + (\frac{\partial L}{\partial \dot{q}} ) \frac{d}{dt}\gamma = \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{q}} \gamma \right) = 0 .
in the first term and combine the two terms
\frac{d}{dt}( \frac{\partial L}{\partial \dot{q}} ) \gamma + (\frac{\partial L}{\partial \dot{q}} ) \frac{d}{dt}\gamma = \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{q}} \gamma \right) = 0 .