Help with non linear problem

[samsus]

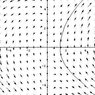
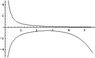
x'=xy
y'=4x+y
solver these both

the first equation can be seprated and end up with ln|x|=(y^2)/2 but then if you solve for y and try to plug into the second equation you get somethin ugly:
y'=4x+sqrt(2ln|x|)

or if you try to find roots you get somethin even uglier y"=4e^(y^2/2)+y


im at a lose at how to do this, can anyone hlep me.
thanks in advance

 

[saltydog]

Hello Samsus. You know, I'm not sure these can be decoupled and solved analytically. Generally, though they're solved both qualitatively and numerically. Are you familiar with Devaney's Differential Equations book? Anyway, other than numerically which is also acceptable, consider the slope field generated by looking at the quotient:

$$\frac{\frac{dx}{dt}}{\frac{dy}{dt}}=\frac{xy}{4x+y}$$

I've plotted this vector field in the phase-plane. That is the x-y plane. It shows how x and y change as functions of t. I've also plotted a particular solution with initial conditions:

x(0)=4

y(0)=-4

Note how the graph travels according to the vector field. Now, this may seem confusing if you're not familiar with this sort of "qualitative" analysis but in a short while, if you work with it, it gives you a very comprehensive picture of how the coupled system behaves on a "global scale".

 

[saltydog]

You know, these can be decoupled:

$$x^{'}=xy\quad\text{(1)}\quad$$

$$y^{'}=4x+y\quad\text{(2)}\quad$$

1. Decoupling x(t):

Solving for y(t) in (1) and taking derivatives:

$$y^{'}=\frac{xx^{''}-(x^{'})^2}{x^2}$$

Substituting into (2) and dividing by [itex]x^2[/tex]:

$$xx^{''}-(x^{'})^2-xx^{'}-4x^3=0\quad\text{(3)}\quad$$
:yuck:

with:

$$x(0)=a\quad\text{and}\quad x^{'}(0)=x(0)y(0)$$

2. Decoupling y(t):

Solving for x(t) in (2) and taking derivatives:

$$x^{'}=\frac{1}{4}(y^{''}-y^{'})$$

Substituting into (1), dividing by 4, and rearranging:

$$y^{''}-y^{'}(1+y)+y^2=0\quad\text{(4)}\quad$$
2x :yuck: = :yuck: :yuck:

with:

$$y(0)=b\quad\text{and}\quad y^{'}(0)=4x(0)+y(0)$$


I know, you're not impressed: out of the frying pan and into the fire.

I think numerically or qualitatively is the best approach with the qualitative method the best for a global perspective. For example, there is a peculiar boundary in the phase portrait in which initial values separated only by an almost infinitessimal amount, lead to very different long-term results. Do you see that?

If the experimental accuracy in determining the initial conditions near this boundary was below this tolerance do you see why it would be impossible to predict the long-term behavior of the system?

 

[saltydog]

For example, there is a peculiar boundary in the phase portrait in which initial values separated only by an almost infinitessimal amount, lead to very different long-term results.

I suspect there might be a little healthy skepticism about that fact. So here goes:

The first plot is for initial conditions:

(20,-11.122)

The second plot is for initial conditions:

(20,-11.123)

This is exhibited in the phase portrait where I've made the difference a little larger to show the different behavior (blow it up to see the two plots for x and y).