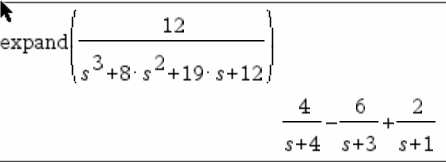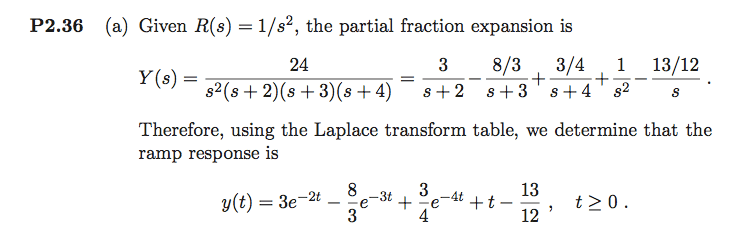Discussion Overview
The discussion revolves around a problem related to partial fraction decomposition in control systems, specifically involving the Laplace transform and transfer functions. Participants are exploring the discrepancies in their calculations and the origins of certain expressions.
Discussion Character
- Technical explanation, Debate/contested, Homework-related
Main Points Raised
- One participant expresses confusion about the origin of the expression R(s)=1/s^2 and its relation to the Laplace transform of a ramp function.
- Another participant clarifies that R(s)=1/s^2 is indeed the Laplace transform of the ramp function r(t)=t.
- A participant notes a potential issue with the problem statement, suggesting that the numbers may have been altered in the source they copied from, leading to inconsistencies with their textbook.
- One participant suggests verifying a partial fraction decomposition by recombining the fractions to check against the original expression.
Areas of Agreement / Disagreement
Participants do not appear to reach a consensus on the problem statement's accuracy, as there are indications of discrepancies between the problem copied and the textbook. The discussion remains unresolved regarding the correct formulation of the problem.
Contextual Notes
There are limitations regarding the clarity of the problem statement and the potential for errors in the source material used by the participants. The discussion also reflects uncertainty about the correct application of partial fraction decomposition in this context.