- #1
1Keenan
- 101
- 4
Hello,
sorry for this stupid question but I am getting confused with equations and I need some help.
My problem is the following:
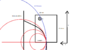
I have a dipole with known magnetic field (B=0.234T), it is 110.6 mm long and 89 mm wide (mechanical dimensions).
I want to calculate deflection of particles (electron with energy E = to 1, 2...30 MeV) and where to expect them on a detector parallel to the long edge of the quadrupole and set at a distance D.
if the detector is behind the magnet I can easily calculate its position, but the confusion I have is that in this case the detecor is on the side and I am going crazy with calculation.
I know energy, and mass, so I know curvature radius in this B=0.234T. I can assume the electrons have main axis in the middle of the magnet, so that they enter at x=0 and their x coordinate at the output would be x=44.5mm. But I am not sure on how calculate the y coordinate and then the angle. In principle if I can get y and angle I can just make it go string and I will know position on the detector... and also some of them might be reflected back if the energy is to low...
Ok, let's put it this way: how to calculatex and y coordinates at the magnet output?
Would you please help me? If my description in not clear I am attaching a sketch.
I could make some quick tracking simulation but I want to solve it analitically first...
Thank you
F.
sorry for this stupid question but I am getting confused with equations and I need some help.
My problem is the following:
I have a dipole with known magnetic field (B=0.234T), it is 110.6 mm long and 89 mm wide (mechanical dimensions).
I want to calculate deflection of particles (electron with energy E = to 1, 2...30 MeV) and where to expect them on a detector parallel to the long edge of the quadrupole and set at a distance D.
if the detector is behind the magnet I can easily calculate its position, but the confusion I have is that in this case the detecor is on the side and I am going crazy with calculation.
I know energy, and mass, so I know curvature radius in this B=0.234T. I can assume the electrons have main axis in the middle of the magnet, so that they enter at x=0 and their x coordinate at the output would be x=44.5mm. But I am not sure on how calculate the y coordinate and then the angle. In principle if I can get y and angle I can just make it go string and I will know position on the detector... and also some of them might be reflected back if the energy is to low...
Ok, let's put it this way: how to calculatex and y coordinates at the magnet output?
Would you please help me? If my description in not clear I am attaching a sketch.
I could make some quick tracking simulation but I want to solve it analitically first...
Thank you
F.