Hi Could anyone of you post here a link to a webpage that actually

  • Thread starter Thread starter dobry_den
  • Start date Start date
  • Tags Tags
    Hi Link
AI Thread Summary
The discussion focuses on understanding how torque applied to a screw translates into a force that drives the screw into a material. When the screw's head is rotated, the shaft also turns, and the thread's groove creates a reactive force that opposes this rotation. This force can be decomposed into components, with one component specifically driving the screw downward. A participant provides a simplified analysis using a free body diagram, confirming that the vertical force is related to the applied torque and thread pitch, while noting that friction is not considered in this basic model. Overall, the explanation emphasizes the mechanics of how screws function through torque and force interaction.
dobry_den
Messages
113
Reaction score
0
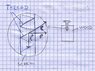
Hi! Could anyone of you post here a link to a webpage that actually describes how a torque (of a screw) is transformed into a force that acts in the direction of the screw's axis, that makes is to screw in? Or could you briefly explain it? Any help would be highly appreciated.
 
Physics news on Phys.org
I mean like.. what makes the screw to go down, to screw in. After I thought about it, I came up with this idea. When I rotate the "head" of the screw, the shaft (the lower part) rotates as well. Since a part of the shaft is already in the wood (where the thread has made a groove), the groove acts against this rotation - reacting with a force F. This force acts on an inclined plane (the thread) and it is possible to decompose it into two forces, F1 and F2. And it is the force F1 that makes the screw to screw in the wood (see the attached drawing).. Is this the appropriate explanation?
 

Attachments

  • screw.jpg
    screw.jpg
    81.1 KB · Views: 508
dobry_den said:
I mean like.. what makes the screw to go down, to screw in. After I thought about it, I came up with this idea. When I rotate the "head" of the screw, the shaft (the lower part) rotates as well. Since a part of the shaft is already in the wood (where the thread has made a groove), the groove acts against this rotation - reacting with a force F. This force acts on an inclined plane (the thread) and it is possible to decompose it into two forces, F1 and F2. And it is the force F1 that makes the screw to screw in the wood (see the attached drawing).. Is this the appropriate explanation?

inclined plane: http://en.wikipedia.org/wiki/Inclined_plane

helically warped, but that is essentially what a screw is: http://en.wikipedia.org/wiki/Screw
 
Last edited:
Yep, I know, so do you think that my drawing is correct?
 
dobry_den said:
Yep, I know, so do you think that my drawing is correct?

I would say you're pretty close. I think you need the equivalent of a "normal" force that is perpendicular to the angled thread. It gets pretty hard to get your head around the helical screw thread, so I did a quick analysis of a much simpler screw, which consists of a bolt with a small post that acts as the thread and a hole with a helical groove cut in it.

The results of the free body diagram confirm the result you get from a "work balance" analysis:

Fvert = 2*pi*T/d

Where Fvert is the vertical force, T is the applied torque, and d is the thread pitch.

This analysis ignores friction, which is a huge simplification. Hope this helps...
 

Attachments

  • screw.jpg
    screw.jpg
    39.1 KB · Views: 546
Thread 'Gauss' law seems to imply instantaneous electric field'

Thread 'Gauss' law seems to imply instantaneous electric field'

Imagine a charged sphere at the origin connected through an open switch to a vertical grounded wire. We wish to find an expression for the horizontal component of the electric field at a distance ##\mathbf{r}## from the sphere as it discharges. By using the Lorenz gauge condition: $$\nabla \cdot \mathbf{A} + \frac{1}{c^2}\frac{\partial \phi}{\partial t}=0\tag{1}$$ we find the following retarded solutions to the Maxwell equations If we assume that...
View full post »

Thread 'Do electron density waves accompany EM waves in coaxial cables?'

Maxwell’s equations imply the following wave equation for the electric field $$\nabla^2\mathbf{E}-\frac{1}{c^2}\frac{\partial^2\mathbf{E}}{\partial t^2} = \frac{1}{\varepsilon_0}\nabla\rho+\mu_0\frac{\partial\mathbf J}{\partial t}.\tag{1}$$ I wonder if eqn.##(1)## can be split into the following transverse part $$\nabla^2\mathbf{E}_T-\frac{1}{c^2}\frac{\partial^2\mathbf{E}_T}{\partial t^2} = \mu_0\frac{\partial\mathbf{J}_T}{\partial t}\tag{2}$$ and longitudinal part...
View full post »

Similar threads

Are Short Links and Weightless Links the Same in Engineering Mechanics?
Replies
13
Views
4K
Considerations for design of lead screw + guide rail set up
Replies
8
Views
4K
B Sign conventions in torque and non-uniform circular motion
Replies
1
Views
1K
B Normal force in case of inclined plane and banked turn
Replies
3
Views
2K
A Advice for 100 MHz resonator
Replies
11
Views
267
I Finding the Axis of Rotation with Given CoG and Force Point
Replies
32
Views
2K
I Trying to calculate the net force/torque of a rock climber on a wall
Replies
4
Views
2K
I Gyroscopic precession of a spin-stabilized bullet
Replies
10
Views
3K
Stats on Students Understanding Theory of Relativity
Replies
4
Views
1K
B Pumping water upwards into a large water tank
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top