Hole Sizing to Drain Fluids [Pressurized Container]

[nn2e19]

Hello,

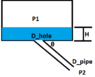
I want to size my system to be able to get rid of fluids without any head buildup within the container. I am just a bit confused as to what formula I should use. My problem is summed up in the following schematic. Note that P1>P2, I have assumed H=10^(-4)m and my flow rate is 0.1 m3/s, dynamic viscosity is 10^(-3) Pa.s. the pipe length is 3.2m. I do not really care about the numbers, I just want to be sure the methodology is correct.

If I use the Bernoulli eqn to size D_hole I use this: Q = Cd*Area*sqrt(2*(g*H+dP/rho)), Area = pi*D_hole^2/4

If I use the same dP and flowrate to get D_pipe I use Q = ((dP-rho*g*L*sin(theta)*pi*D^4)/(128μL))

I'm just baffled as to which one is more suitable for my problem.

Any help is greatly appreciated.

 

[jrmichler]

In your case, the total head is the vertical distance from the fluid surface to the discharge end of the pipe. The method I use for calculating flow rate is as follows:

1) Assume a flow rate.
2) Calculate the pressure drop through an orifice diameter equal to the pipe ID.
3) Calculate the head loss through the pipe. I use a Moody diagram for this.
4) Sum the two losses.
5) Iterate as needed until the calculated head loss matches the actual head. That's your flow rate.
6) Remember that any pressure/vacuum in the container is part of the head loss calculation.

Hint: With your dimensions, the head loss will be approximately proportional to the square of the flow rate. Use this in your iteration.