Please tell me the difference in the size of the air volume

[Hauzen]

Hi.
Since I've been studying fluid mechanics, I've been asking a lot of questions
Thank you all for your help!

I suddenly have a problem that I want to think about while studying today.
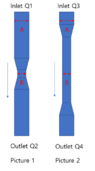
I would like to know the change of air volume according to the pipe shape as shown in the picture below
Condition 1) Fan is installed below and air is flowing downward.
Condition 2) The cross-sectional area of the two pipes is the same as A and the narrow areas are the same as B.
Condition 3) Compared to Photo 1, Photo 2 has a longer narrow diameter.
Condition 4) There is a pipe friction coefficient.
Condition 5) Q2=Q4
Q1,Q3 How do I list them in order of the most air volume?
I think it will be easier to understand if you use a formula to prove it, so please help me

 

[erobz]

If the fan is the same, which piping has more frictional resistance in your estimation? Experiment. Try sucking air through a straw, and a paper towel tube. In order to understand which would have higher flow rate you have to understand the how the fan and the system interact. This requires you to examine the fan performance curve, and system resistance curve.

 

[Hauzen]

Thank you for your help every time.
It seems like you're learning a lot.

I accidentally didn't put a condition on it. condition It's the same as Q2=Q4.
Theoretically, the case of ideal fluids seems to be Q1=Q3.
I think it's Q1>Q3 when I think about the straw.
I'd like to prove the content with a formula.

Are you saying that we need to study the fan performance curve and system resistance curve you mentioned to prove this?

 

[erobz]

I accidentally didn't put a condition on it. condition It's the same as Q2=Q4.
Theoretically, the case of ideal fluids seems to be Q1=Q3.
I think it's Q1>Q3 when I think about the straw.
I'd like to prove the content with a formula.

Are you saying that we need to study the fan performance curve and system resistance curve you mentioned to prove this?

If we have approximately incompressible flow, and $Q_1 = Q_3$ then it necessarily follows that $Q_2 = Q_4$. In fact $Q_1 = Q_2 = Q_3 =Q_4 = Q$ !

What is different between the systems for a particular flowrate "$Q$" passing through either one is the pressure at the inlet, assuming the outlet's are atmospheric pressure.

Thank you for your help every time.
It seems like you're learning a lot.

I'm trying my best to answer your slight variations on this question with the three threads you created, but you are having trouble with this concept.

I'd like to prove the content with a formula.

I already showed you the formula in the last thread.

Are you saying that we need to study the fan performance curve and system resistance curve you mentioned to prove this?

A fan has a "performance curve" (Pressure Output vs Flow), and a piping system has a "system curve"( Pressure Loss vs Flow). The point of intersection of these two curves is the steady state operation point of that fan and that piping. If the same fan is in the system on the left it will have run a different flowrate than if the same fan was in the system on the right. Hence same fan, different piping system means $Q_1 \neq Q_3$.