Horizontal to tilted beam radiation

[StGoldfinkle]

Hello, the name's Mike and I'm a newbie here,

I have a question pertaining to solar angles required to calculate a solar panel's hourly generation over one year. Total solar irradiance on a tilted surface equals the sum of the direct, diffuse and reflected component. In my case, reflection is assumed zero and the diffuse and direct horizontal components have been calculated.

The problem is the conversion of the direct horizontal component to its tilted counterpart. For this, I calculate the hourly ratio Rb (cosine of incidence over cosine of zenith). The horizontal component times Rb equals the direct tilted component.
The problem however is that this ratio Rb becomes incredibly large at times due to the zenith angle's cosine being small enough with respect to the corresponding incidence cosine.

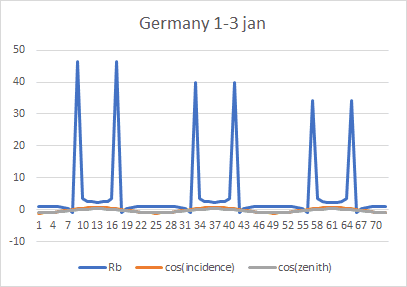
This results in an hourly global tilted irradiance (Wh/m2) as such:

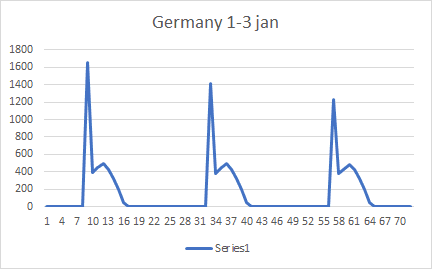
Such peaks are just not realistic and I can't seem to find a solution to this problem. This issue occurs nearly every day for all areas. Does anyone have an explanation as to what I'm missing?

Thank you in advance,

Mike

 

[sophiecentaur]

Hi and welcome to PF.

I am not sure what the problem is, exactly and I don't understand what those graphs represent. What is the 'tilted counterpart'? There will be only one maximum as the Sun passes over the panel (- won't there?). Are you looking at the problem in the right way?
The power out of a PV panel will be affected by the directivity of the individual cells but I thought that PV arrays were arranged to have a more or less hemispherical pattern. So the power out, directly from the Sun will be more or less proportional to the projected area of the panel in the direction of the sun. That will be Acos(θ) where A is the area and θ is the angle and will be a wide curve, rather than the sharp peaks that your graphs imply. The angle will be a combination of the azimuth and elevation of the sun at any time.
Is it not as simple as that - or is it going over my head? (like the Sun haha)
I assume you have looked around at the massive amount of sources on the Web about this.

 

[StGoldfinkle]

Hi Sophiecentaur,

First off, thank you for your response. My apologies for the lack of clarity. I'll try to explain better. Note that the following description is how I have understood the large amount of sources on the web regarding these calculations. Also, this would be a massive post if I explained every angle therefore apologies if I appear to cut corners. I'm really dying to know what I'm doing wrong.

The goal is to calculate the hourly incident radiation on a tilted surface over the course of one entire year for 9 different zones in Western Europe.
To calculate the radiation incident on a tilted surface, there are three components of radiation that need to be calculated and added together: the tilted beam irradiance, tilted diffuse irradiance and tilted reflected irradiance. The reflected part is assumed to be zero. The diffuse part is a pretty easy and straight-forward calculation. The tilted beam irradiance needs to be calculated using the horizontal beam irradiance which is extracted from a dataset of global horizontal irradiance provided to me. To convert from horizontal to tilted beam irradiance, the horizontal irradiance has to be multiplied by the factor Rb. This factor equals cos(theta)/cos(thetaZ), or cos(incidence angle)/cos(zenith angle) where the cos(theta) equals:

and cos(thetaZ) equals:

delta is the declination angle, phi is the location's latitude, beta is the solar panel's tilt angle, Azs is the solar panel's azimuth angle and omega is the hour angle.

All these angles have been calculated using the, as you put it, massive amount of sources on the web. Now, the calculated Rb reaches infinity at 2 moments per day as thetaZ, the sun's zenith angle is 90° at 2 points during the day. As an example, below is a figure showing both cosines for the first 3 days for a location in Germany:

As you can see, the cosine of the zenith angle passes the zero mark at 2 moments each day, meaning the Rb ratio reaches infinity. This means that any beam horizontal irradiance is bloated to an infinite amount of beam tilted irradiance. This in turn causes massive incident radiation peaks at sunrise and sunset. Therefore I believe I'm doing something wrong. However I can't seem to find a great deal about this ratio or any figures showing these angles and cosines, so I resorted to the good people of the PhysicsForums.

Just in case someone is hell-bent on helping me solve this, the clearest and most concise sources regarding these calculations are the following two links:
http://www.itacanet.org/the-sun-as-a-source-of-energy/part-3-calculating-solar-angles/
http://www.enhems-buildings.fer.hr/_download/repository/EDPE13_[Gulin,_Vasak,_Baotic].pdf

Again, thank you for taking the time to respond, I hope this clears up what my problem is. I also hope I'm not doing something incredibly stupid and obviously wrong. I thought it was a significantly more straight-forward calculation.. I was wrong haha.

 

[sophiecentaur]

Those links have made things clearer, thanks. The diagram makes sense and the equations seem fair enough to my brief look. (Potentially, I think I could find my way to them - you know what I mean!)
I looked at your graphs at the top, with those pairs of peaks, and the peaks occur around sunrise and sunset when the sun is only grazing the panel. That apparent magnification factor is only relevant when there is virtually no area of panel receiving sunlight. If you multiply your Rb by the cos of the incidence angle, what do you get? (along the lines of 0 times ∞)
Those references seem to be attempting to squeeze the last drop of energy out of what's available, which is way more than the average installation is based on - as you will know. (We usually just accept that a low Sun will not give us any Power, don't we?) I am not sure where the basic initial statement I made departs from your analysis in the range of significant Power output. Allowing that the irradiance at a point on the Earth will vary because of the atmosphere's thickness, why is there anything more to the problem at high angles of incidence on the panel (near 90°)?
Just examining the geometry of the situation (the rest isn't involved with your problem affaics):
I have a problem with the physical significance of your R_b. It's the ratio between the cos of two angles which spells possible trouble for a start. The equation 3.12 in the ITCA link seems to give you the angle of incidence without any of your 'funny business' from dividing by zero. Isn't that all you need to know for the projection of the panel from the Sun? I may well have totally missed what you are getting at but my view seems to agree with what we actually experience and I do like a tidy life.
Perhaps I am just being too rough and ready about this but it's possible you are worrying too much about what happens under a limited set of conditions.

 

[StGoldfinkle]

I had the same thought about the physical significance of this Rb, something's iffy about it. You say that the magnification factor is only relevant when there is virtually no area of panel receiving sunlight. As I understood however, this Rb magnification factor in a way "converts the area of a flat panel receiving sunlight to the area of a tilted panel receiving sunlight". Therefore it is relevant at all times of "daylight".

Equation 3.12 you refer to calculates the solar zenith angle which equals the angle of incidence only for flat, zero-tilt panels. There is also equation 3.13 but this is not an option as I want to evaluate the power output for solar panels directed to the east and west as well as to the south, meaning equation 3.11 has to be used (3.13 is just a simplified 3.11 anyway). Using equation 3.12 means I would be neglecting the panel's tilt completely, and the Rb ratio would just be cos(thetaZ)/cos(thetaZ) = 1 across the board. As the other paper linked in my previous post shows in equations 2 to 4, both the angle of incidence for a tilted and horizontal panel (the last one equals the solar zenith angle) are required to calculate the tilted beam irradiance.

Again my apologies if I'm missing a part of your explanation. This paper and many others follow the same logic and equations, therefore I cannot believe this is a problem the authors and others have experienced. Either I'm doing something wrong in my calculations (which I have checked numerous times) or Rb ratios of 10.000 actually exist but are exclusively present at times of zero incident radiation (this would still bug me though). Just following the equations one by one as provided by all these sources, I get large Rb's in the mornings and evenings. This Rb thing is a purely geometrical problem. If you don't mind me asking: what would you do in this case? No source elaborates on this issue and I cannot just assume zero incident radiation at all these mornings and evenings as this would mean I'm shortening winter daylight duration by 25% if you understand what I mean.

 

[sophiecentaur]

Equation 3.12 you refer to calculates the solar zenith angle which equals the angle of incidence only for flat, zero-tilt panels.

Sorry, actually it's 3.11 that is what you need. It gives Cosθ_i and it says that θ_i is the incident angle on the panel. I can't imagine why he deals with those two 'special' angles. Neither would be what a solar panel installer would use (not in the UK at least). Perhaps on the top of a vehicle . . . .
He says it's a "horrible equation" but that's no problem for a computer to deal with and it's the appropriate one, surely.
If the panel were out in space, it would absorb the energy falling on it and that would be the flux density times the projected area (A cos (θ). What is different at ground level - except for the additional atmospheric absorption factor, which depends on the incident ray path through the atmosphere? (I'm not including the scattered contribution, of course) It strikes me that you may be trying to do the same calculation twice. How is it any more than simple geometry?

 

[sophiecentaur]

I have ben looking in more detail at the longer of the two papers. R_b is just a bit of maths and I think it just tells you that a tilted panel can do a lot better than a horizontal panel when the horizontal panel is picking up very little. The factor of 50 doesn't mean that you will get a lot of Power out; it just means that you will get more than a very little at sunrise and sunset if the panel is tilted a bit.
That long paper is typical of such publications as it is not aimed at the casual reader but someone who is in the business. There's no reason why they couldn't have explained what those curves you have plotted actually imply. The paper is very theoretical and I don't see how their method would ever be better than one based on thousands of measurements of actual arrays could yield. Why use neural networks, I wonder? It is possible that someone was looking for an application for their favourite system and collaborated with someone involved in solar energy.
They mention Solar tracking but, if they are going to the trouble of a motorised array, why not do real time optimisation of the pointing direction, which would take account of total (including temporary lighting conditions)? I know nothing of the background of their work but I do know about engineering and human nature. "Do it my way" is a very strong motivation for some choices.

 

[sophiecentaur]

I was playing with two sheets of paper, representing a horizontal panel and a tilted panel. Viewing them from various directions, corresponding to the Sun's position during the day tells you how much flux is intercepted by each as the projected areas change with time. At a relatively high latitude (as in Germany or UK) there can be a high ratio between the projected areas. In the sunrise situation, the horizontal panel intercepts none but the tilted panel intercepts a finite amount. Both projected areas are small, of course but the ratio is high.
It's a worthwhile exercise, if the trig is suggesting something that is not intuitive. Irradiance , rather than flux density makes appreciating what happens a lot harder (for me at least).
PS there are tilt angles that will give you a lower projected area but the ratio is less than 1 so the minimum is not peaked so it's not noticeable.

 

[Nefk]

Hello ! My name is Nick. I encounter the same problem with you. Finally, how did you solve it ?

 

[Demolli16]

Hi, I have same problem! I want to ask you how did solved it: