DaveC426913
Gold Member
- 23,886
- 7,916
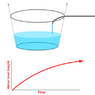
I am filling my circular hottub, and charting the water level height. Its sides have a small, constant slope from vertical - i.e. it is a truncated, inverted cone.
Imagining an ideal hottub of unlimited height*, the water level will always be increasing - but at a decreasing rate - it will level off more and more over time.
So it can't be an asymptote, since it will never reach a limit. Then again, it will also never stop curving.
What is this curve?*OK, that's not an ideal hottub in my eyes. Easy to drown.
Imagining an ideal hottub of unlimited height*, the water level will always be increasing - but at a decreasing rate - it will level off more and more over time.
So it can't be an asymptote, since it will never reach a limit. Then again, it will also never stop curving.
What is this curve?*OK, that's not an ideal hottub in my eyes. Easy to drown.