scottypippen
- 1
- 0
Three displacement vectors of a croquet ball are shown in the figure, where || = 10.0 units, || = 35.0 units, and || = 10.0 units.
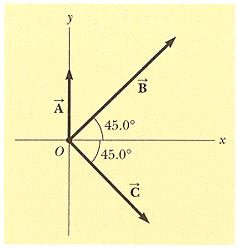
(a) Find the resultant in unit-vector notation.
(b) Find the magnitude and direction of the resultant displacement.
For part a, I broke each down vector into its compnents:
Va: <0,10>
Vb: x = r Cos o y = r Sin o
x = (35) cos 45 y = (35) sin 45
Vb = <24.75, 24.75>
Vc: x = 10 Cos 45 y = 10 Sin 45
= <-7.07,-7.07>
Using the head to tail method, I simply added all the Vectors and got the Resultant vector as:
17,7i + 27.7j
For part b I used pythagorean's to find the magnitude which came out to:
(17.7^2 + 27.7^2)^1/2 = 32.8
Then I used inverse of Tan (27.7/17.7) which came to:
57.4 degrees
I'm almost certain this is correct but webassign keeps saying its wrong! Any help or input is greatly appreciated, thanks.
(a) Find the resultant in unit-vector notation.
(b) Find the magnitude and direction of the resultant displacement.
For part a, I broke each down vector into its compnents:
Va: <0,10>
Vb: x = r Cos o y = r Sin o
x = (35) cos 45 y = (35) sin 45
Vb = <24.75, 24.75>
Vc: x = 10 Cos 45 y = 10 Sin 45
= <-7.07,-7.07>
Using the head to tail method, I simply added all the Vectors and got the Resultant vector as:
17,7i + 27.7j
For part b I used pythagorean's to find the magnitude which came out to:
(17.7^2 + 27.7^2)^1/2 = 32.8
Then I used inverse of Tan (27.7/17.7) which came to:
57.4 degrees
I'm almost certain this is correct but webassign keeps saying its wrong! Any help or input is greatly appreciated, thanks.