How can a ball rise higher than originally dropped?

[FallenApple]

So here is a case where a ball is thrown on the floor with no friction.

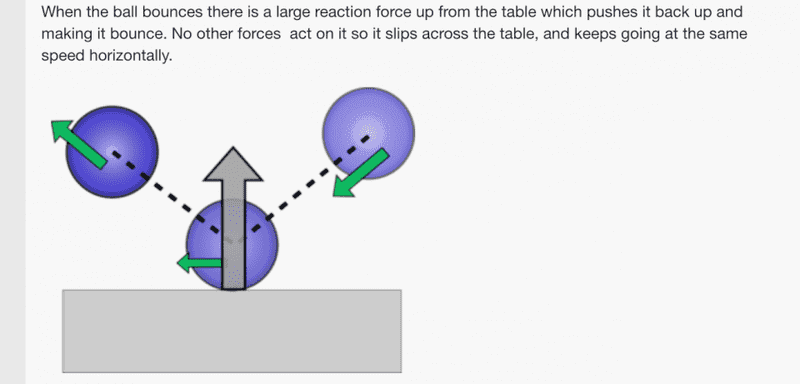Then is a case with friction

Now what I don't understand is how is the presence of friction going to make the normal force larger than usual. The friction is dependent on the normal force, not the other way around. And the normal force is dependent on the vertical impulse, which should the same as the previous case, since the CM of the ball has the same final vertical velocity before impact.

 

[Guy Madison]

Well there is angular momentum, the ball when it hits a surface with friction will convert angular momentum into deformation so that would account for an additional boost.

 

[jbriggs444]

Now what I don't understand is how is the presence of friction going to make the normal force larger than usual. The friction is dependent on the normal force, not the other way around. And the normal force is dependent on the vertical impulse, which should the same as the previous case, since the CM of the ball has the same final vertical velocity before impact.

You are correct. The normal force would not be larger than normal. But I think that you are misinterpreting the drawing. It is not intended to show that the bounce is reaches a higher maximum height than normal. It is intended to show that the bounce angle is higher than normal.

You can achieve a higher bounce angle in either of two ways: By reducing the horizontal velocity or by increasing the vertical velocity. The text speaks of the former and not the latter.

 

[FallenApple]

You are correct. The normal force would not be larger than normal. But I think that you are misinterpreting the drawing. It is not intended to show that the bounce is reaches a higher maximum height than normal. It is intended to show that the bounce angle is higher than normal.

You can achieve a higher bounce angle in either of two ways: By reducing the horizontal velocity or by increasing the vertical velocity. The text speaks of the former and not the latter.

Oh ok. That makes sense. The height must be the same, so the reduced distance(due to friction) traveled in the x direction would cause the hypotenuse to be angled higher.

 

[A.T.]

You are correct. The normal force would not be larger than normal. But I think that you are misinterpreting the drawing. It is not intended to show that the bounce is reaches a higher maximum height than normal. It is intended to show that the bounce angle is higher than normal.

You can achieve a higher bounce angle in either of two ways: By reducing the horizontal velocity or by increasing the vertical velocity. The text speaks of the former and not the latter.

The question remains if the friction-ball can actually jump higher (achieve higher vertical velocity) than the frictionless ball. Without initial rotation, the friction-ball loses linear KE to rotational KE, so the final linear speed is lower than for the frictionless ball. Can the vertical velocity still be higher for the friction-ball, due to the steeper angle? Consider the extreme case of a very flat initial angle.

 

[Nugatory]

Can the vertical velocity still be higher for the friction-ball, due to the steeper angle?

I believe so - no conservation law is violated if you include the Earth so that the system is properly closed with regard to conservation of angular and linear momentum.