How Can I Calculate the Sheet Resistance of a Metal Mesh with My Measurements?

[Angino]

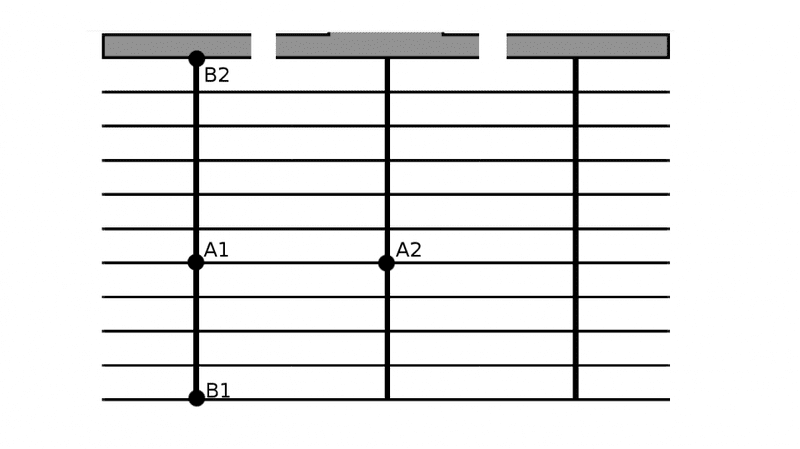
I would like to know the sheet resistance of a metal mesh that consists of 3 larger busbars (W=0.0025 cm L=0.3 cm) and 10 smaller fingers (W= 0.0002 cm L= 0,16416 cm) which are all connected by a big collection bar. The thickness of the whole layer is 0.00. This collection bar has been interrupted for the sake of measurement as seen in the picture. The measurement of the small finger has been done with 2 point measuremnt at the points A1 and A2. The measurement of the busbar has been done with point B1 and B2.

The finger has a resistance of 33.34 Ω.
The busbar has a resistance of 40.8Ω.

Usually one would measure the sheet resistance with a 4 point probe or with eddy current to eliminate the contact resistance, however i don't have the equippment.

I don't quite understand how i can calculate the sheet resistance of a film with "holes"

Sheet resistance is calculated by

Rs = R*W/L

Rs = sheet resistance
R = resistance
W = Width of the measured area
L = length of the measured area

To my understanding that would yield the sheet resistance of the finger or the busbar only (thus a continuous film)

Is it possible to calculate the sheet resistance of the entire mesh with my measurements? If so, how? I am not able to wrap my head around it.

 

[Archie Medes]

Never done a problem like this, but here's my thoughts

The mesh is basically a rectangular grid of individual resistors, from which the extremities (apart from that at B2) can be ignored. I am also assuming there is no electrical connection between the three busbar ends beyond the final finger at the top of the diagram. As a thin film, I am also assuming sheet resistance Rs is constant throughout the mesh. So the circuit becomes:

Rs = Rv*Wv/Lv = Rh*Wh/Lh

Now you have Rv in terms of Rh (or vice versa), solve the mesh equivalent resistance between a set of points, and you can get Rs

*edit - actually, that's too simple, I'm treating the junctions as points with no area and zero resistance

 

[Angino]

Hello Archie Medes,

thank you for your thoughts.

I am also assuming there is no electrical connection between the three busbar ends beyond the final finger at the top of the diagram

This is correct.

As a thin film, I am also assuming sheet resistance Rs is constant throughout the mesh

This is also correct.

The actual application of that mesh is a solar cell, which means, that this electrode will have electrons injected everywhere on its surface of one side relatively equally, which is why i don't think the fingers on the outer edge can be ignored, since they contribute current to the busbar.

The sheet resistance of a continuous film of that material with that thickness should be 0.35 ohm/sq according to Rs = R*(W/L) when using the values from the busbar.

As far as I am aware, sheet resistance is defined as having the same value no matter how big the square regarded is. Thus if the sample is 3x5 mm we effectively have 1,6666 squares and thus a resistance of 0.58 ohm if the current flow direction is horizontal or 0,2333 ohm/sq if the flow direction is vertical. In this case however the flow direction is vertical and horizontal.

Regarding the mesh as a grid of individual resistors is a good idea, however, when calculating the resistance that way, i will not be taking into account that the electrons encounter a short or a long path before reaching the collection bar.

But does that even matter? Maybe i suffer from a fundamental misunderstanding.

 

[Archie Medes]

I'm afraid you would have a better understanding of it than I would. I don't actually know anything about the physics of photovoltaics.

My grid suggestion would only give a reasonable answer if the resistance of Rv and Rh were both significantly higher than the junction resistance, and whether measuring the resistance of the photovoltaics behaves the same way as measuring normal resistance.