Jonobro
- 7
- 0
Problem
Let X be a uniform(0,1) random variable, and let Y=e^−X.
Find the CDF of Y.
Find the PDF of Y.
Find EY.
Relevant Equations
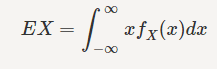
http://puu.sh/kAVJ8/0f2b1e7b22.png
My attempt at a solution
If I solve for the range of y I get (1, 1/e), but because Y is not an increasing function, my second bound is smaller than my first. I am really confused as to how I would be able to solve for the CDF and PDF in this case... Any help would be greatly appreciated.
Let X be a uniform(0,1) random variable, and let Y=e^−X.
Find the CDF of Y.
Find the PDF of Y.
Find EY.
Relevant Equations
http://puu.sh/kAVJ8/0f2b1e7b22.png
My attempt at a solution
If I solve for the range of y I get (1, 1/e), but because Y is not an increasing function, my second bound is smaller than my first. I am really confused as to how I would be able to solve for the CDF and PDF in this case... Any help would be greatly appreciated.
Last edited by a moderator: