How can I find the inertia of a rod with a pivot point?

[Blockade]

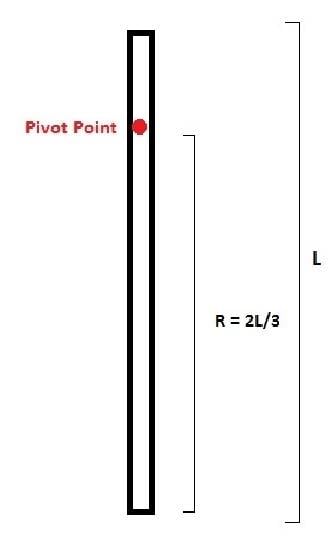
I have a question on finding the inertia of a rod with a pivot point somewhere along it's length.

So the inertia of a rod is I_{Stick cm} = 1/12 *m*L²
Does L² = (2L/3)² = 4L²/9 -> 1/12 *m*[4L²/9] or is it something like
m*L²/12 + m* (2L/3)²?

If it's the second one then may I ask why it's that?

Picture

 

[Let'sthink]

Revise parallel axis theorem; I = Ic + (md^2) Ic is MI about CM and d is the distance between parallel axes passing through CM and pivot. It can be proved first and then can be used.

 

[Blockade]

Revise parallel axis theorem; I = Ic + (md^2) Ic is MI about CM and d is the distance between parallel axes passing through CM and pivot. It can be proved first and then can be used.

so m*L2/12 + m* (2L/3)2
where Ic = m*L2/12
and md^2 = m* (2L/3)2when you said "MI about CM" you mean the mass around the center mass which is the entire rod? As for d is the "distance between parallel axes passing through CM and pivot" meaning the length between the end of the stick pass the center mass where it ends at the pivot?

 

[Let'sthink]

center of mass is at the mid point of rod at L/2 from one end and if pivot is at 2L/3 from one end then d = (2L/3) - (L/2) = L/6. Ic is the MI about the axis passing through the point at L/2 from one end.