Discussion Overview
The discussion centers on calculating the moment of inertia of a rod with a pivot point located along its length. Participants explore the application of the parallel axis theorem and the implications of different pivot placements on the inertia calculation.
Discussion Character
- Technical explanation
- Mathematical reasoning
Main Points Raised
- One participant questions whether the moment of inertia should be calculated as IStick cm = 1/12 * m * L² or if it involves additional terms due to the pivot point's location.
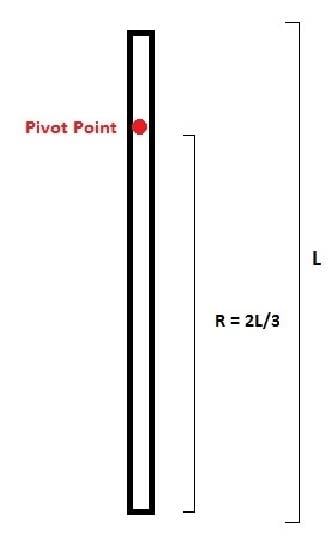
- Another participant suggests revising the parallel axis theorem, stating that I = Ic + (md²), where Ic is the moment of inertia about the center of mass and d is the distance between the parallel axes.
- Further clarification is sought on the meaning of Ic and the distance d in relation to the pivot point and the center of mass.
- A participant identifies the center of mass as being at L/2 from one end and calculates the distance d as L/6 when the pivot is at 2L/3 from one end.
Areas of Agreement / Disagreement
Participants express differing views on the correct approach to calculating the moment of inertia, indicating that multiple competing models and interpretations remain unresolved.
Contextual Notes
There are limitations regarding the assumptions made about the pivot point's location and the definitions of terms used in the calculations, which have not been fully resolved.