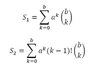hddd123456789
- 92
- 0
Hi,
I'm trying to see if there is an operation or set of operations I can perform on S1 so that it equals S2. I've just been going in circles and it seems I just don't have enough knowledge of how factorials behave in series to crack this. Any hints would be much appreciated.
Hope this makes sense.
Thanks!
I'm trying to see if there is an operation or set of operations I can perform on S1 so that it equals S2. I've just been going in circles and it seems I just don't have enough knowledge of how factorials behave in series to crack this. Any hints would be much appreciated.
Hope this makes sense.
Thanks!