How Can I Prove AH = DK in Triangle Congruency?

  • MHB
  • Thread starter Yazan975
  • Start date
In summary, to prove congruency between AH and DK, we must show that they have equal lengths and equal angles using methods such as SAS or ASA. This allows for confident use and accurate calculations between the two objects. Other methods of proving congruency include HL and SSS, but SAS and ASA are most commonly used. Congruency can also be proven between other geometric figures, and it has real-life applications in fields such as architecture, engineering, and computer graphics.
  • #1
Yazan975
30
0
View attachment 8758View attachment 8759

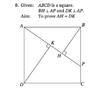
This is where I got so far. I can't figure out how to prove AH = DK in order to prove the HL property of congruency
 

Attachments

  • Screen Shot 2019-01-26 at 11.20.23 AM.png
    Screen Shot 2019-01-26 at 11.20.23 AM.png
    18.1 KB · Views: 62
  • Photo on 1-26-19 at 11.15 AM.jpg
    Photo on 1-26-19 at 11.15 AM.jpg
    26.9 KB · Views: 63
Mathematics news on Phys.org
  • #2
I'm assuming you need to prove $\overline{AH}=\overline{DK}$.

After proving $\triangle{ADK}\cong\triangle{ABH}$ what can you say about the sides of these two triangles?
 

FAQ: How Can I Prove AH = DK in Triangle Congruency?

How do you prove AH=DK using congruency?

In order to prove that AH=DK using congruency, you need to show that the two triangles, triangle ADH and triangle DCK, are congruent. This can be done by showing that they have the same corresponding angles and sides.

What is the first step in proving AH=DK using congruency?

The first step is to identify which triangles need to be proven congruent. In this case, it is triangle ADH and triangle DCK.

What are the different methods of proving AH=DK using congruency?

There are several methods that can be used to prove AH=DK using congruency, such as side-angle-side (SAS), angle-side-angle (ASA), side-side-side (SSS), and hypotenuse-leg (HL).

What are the key properties of congruent triangles that are used to prove AH=DK?

The key properties of congruent triangles are the reflexive property, which states that a triangle is congruent to itself, and the corresponding parts of congruent triangles are congruent (CPCTC).

Can you prove AH=DK using congruency if only some of the corresponding angles and sides are known?

No, in order to prove AH=DK using congruency, all of the corresponding angles and sides must be known and shown to be equal. It is not possible to prove congruency with only some information.

Similar threads

I (Elementary number theory) Understanding congruence and modulus
Replies
9
Views
1K
I Chiral symmetries in E[SUP]^n[/SUP]
Replies
1
Views
1K
MHB Can you prove that Triangle $ABC$ is Isosceles?
Replies
1
Views
1K
[IntroNumTheory] Determining the remainder by using congruence
Replies
1
Views
892
MHB Proving Triangle Area ≤ $\frac{1}{2}$ in a Square with $(n+1)^2$ Points
Replies
1
Views
976
MHB Proving Orthogonal Projection of Triangle V, v'_{1}
Replies
1
Views
895
I Given a triangle ABC, on which side of the triangle does the point D lie?
Replies
6
Views
2K
MHB Equilateral triangle within a circumscribed circle
Replies
5
Views
3K
I How to Prove a Congruence Relation for Prime Numbers?
Replies
17
Views
2K
MHB Prove that triangle BAD is isosceles and....
Replies
4
Views
2K

Hot Threads

Recent Insights

Back
Top