3123marriott
- 1
- 0
if anyone can do this i will be very happy I've had a good old try and i end up just lost in variables
i would like to re-arrange to make apipe the subject
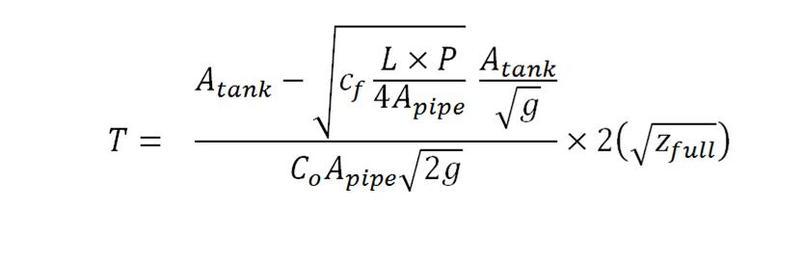
i ended up with the sqrt of one apipe which i don't know how to solve;
thanks
i would like to re-arrange to make apipe the subject
i ended up with the sqrt of one apipe which i don't know how to solve;
thanks
Last edited: