bmb2009
- 89
- 0
Homework Statement
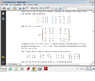
The problem is attached due to it not being able to copy over the given matrix..
Number 5.3
Homework Equations
The Attempt at a Solution
I tried to compute A+tI and then row reduce until A+tI was a triangle matrix and then multiply the diagnol entries but I got stuck.. any help would be great! thanks!