Spanky Deluxe
- 19
- 0
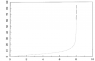
I need to work out an equation (and also the gradient) of the attached graph for use in a toy model. Alas I don't have stuff like Mathematica here and I don't normally do this kind of thing so I've just been stuck to using Grapher to chuck random equations in and Excel to try to plot points for it to generate an equation.
I don't need anything exact, just something that looks roughly the same but I can't recognise any functions that could create something like this.
Any ideas?
I don't need anything exact, just something that looks roughly the same but I can't recognise any functions that could create something like this.
Any ideas?