How Can We Calculate the Distance Traveled by a Coin in a Physics Experiment?

  • Context: Undergrad 
  • Thread starter Thread starter smslca
  • Start date Start date
  • Tags Tags
    Distance traveled
Click For Summary

Discussion Overview

The discussion revolves around calculating the distance traveled by a coin in a physics experiment involving forces, motion, and rotational dynamics. Participants explore the application of mechanical physics principles to a specific experimental setup, focusing on the variables involved and the formulation of the distance traveled by the coin.

Discussion Character

  • Exploratory, Technical explanation, Debate/contested, Mathematical reasoning

Main Points Raised

  • One participant describes an experiment involving a coin placed on the edge of a laptop and questions how to compute the distance traveled by the coin after applying a force.
  • The participant identifies known variables such as the radius of the coin, the distance supported by the laptop, and the time taken to stop, but struggles to determine the initial velocity.
  • Another participant asks for clarification on the direction of the force acting on the coin, confirming it is a downward force.
  • A later reply suggests that if the coin does not slip, it will rotate around the edge of the laptop, and encourages calculating the velocity of the center of mass at that instant to find the initial velocity.
  • The same reply also raises the possibility that the coin may slip, complicating the calculations further, especially if the edge of the laptop is not sharp.

Areas of Agreement / Disagreement

Participants express differing views on the behavior of the coin during the experiment, particularly regarding whether it will slip or rotate without slipping. There is no consensus on the best approach to calculate the initial velocity or the distance traveled.

Contextual Notes

The discussion includes assumptions about the behavior of the coin, such as whether it slips or rotates, and the implications of these assumptions on the calculations. The complexity of the situation is acknowledged, particularly regarding the shape of the edge of the laptop and the forces involved.

Who May Find This Useful

Readers interested in mechanical physics, experimental design, and the application of forces in motion may find this discussion relevant.

smslca
Messages
63
Reaction score
0
A rough sketch of experiment.
14t4sk5.png

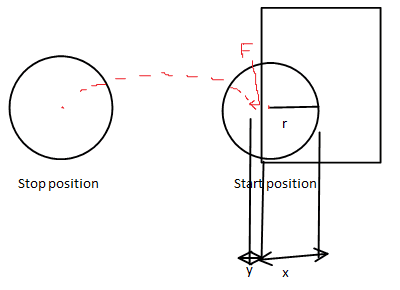
the red dots represent a side view of path traveled, F is downward force and the tool used here is a pen placing parallel to the coinHi. I have newly started to study mechanical physics. based on study, I conduct a simple experiment. But unfortunately i am unable apply the laws in reality.

Experiment:
I placed a coin(2 Indian Rupee coin) with radius "r" positioned flat part of coin parallel to base of my laptop. Also placed at edge of base such that "x mm" of diameter of coin is supported by laptop while 2r-x is free, unsupported with the coin in a balanced position. Now at "x+y mm < r" measured from center of coin toward the free end I applied a random force perpendicular to laptop base.

Now my question is , how can we compute(formulate) distance "z" traveled by coin measured from center of coin at start point to center of coin at the place it stopped in terms of known variables mentioned below.

My attempt:
To me the known values are : r,x,y,density of coin(p),width(or height) of coin(w),time it took to stop(t).
Here for simplicity I have not considered the torque generated, and visualized the traveled path as a simple parabolic path. Now I can measure the distance traveled
z = v0t+(1/2)gt2. where g is acceleration due to gravity.

But how can I find the initial velocity v0. I know v0 is not zero, since the situation here is not equivalent to a freely falling scenario.
 
Last edited:
Physics news on Phys.org
Is the force acting up or down?
 
mikeph said:
Is the force acting up or down?

It's a downward force.
 
hi smslca! :smile:

assuming the coin doesn't slip, it will rotate around the edge of the laptop until the reaction force is zero

calculate the velocity (magnitude and direction) of the centre of mass at that instant: that is your vo and θ :wink:

(but it probably will slip, and if the edge is curved not sharp then that makes the maths even more difficult)
 

Similar threads

Undergrad Distance traveled by a ball down a ramp and on a flat path
  • · Replies 12 ·
Replies
12
Views
3K
Undergrad How Can Gravity Affect Distance Traveled in a Coding Simulation?
  • · Replies 5 ·
Replies
5
Views
5K
Undergrad Guitar String Maximum Travel Distance
  • · Replies 4 ·
Replies
4
Views
3K
High School Applying the distance formula d= v*t + 1/2a*t^2
  • · Replies 5 ·
Replies
5
Views
8K
Undergrad Do smells travel farther in colder or hotter temperatures?
  • · Replies 8 ·
Replies
8
Views
3K
Tracking travel between orbits in a whirlpool
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad The Feynman way of explaining Symmetry in Physical laws
  • · Replies 45 ·
2
Replies
45
Views
4K
Undergrad Paper Plane Distance Experiment: Power & Energy Calculation
  • · Replies 5 ·
Replies
5
Views
2K
Undergrad Distance travelled with constant increasing force
  • · Replies 17 ·
Replies
17
Views
3K
Undergrad Spacetime distance and ruler-measured length on an XT chart
  • · Replies 6 ·
Replies
6
Views
2K