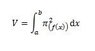How can we use calculus to find volumes of revolution?

[Endorser]

As part of an assignment on Approximating Areas and Volume I am asked to derive the equation shown in the image attached.

The question reads: "It can be shown that if y = f(x) is revolved around the x-axis to form a solid between x=a and x=b then the volume of the solid is give by the equation shown in the image.

Some equations I have been using are basic area formula such as
Area (trapezium) = 1/2(a+b)xh

I have also attempted to derive the forumula by looking at the Trapezoidal Rule and Simpson's Method and working backward to derive the formula.

 

[mattg443]

As you rotate a cross section of the curve around the axis, it forms a cylinder, with radius y=f(x). and a thickness of δx.

The volume of that cylinder is given by:
A=\piy² δx

As the thickness of the cylinder approaches zero and you add (integrate) all the volumes of the reaaaaaly thin cylinders.
That gives the expression:

\int\pif(x)²dx

I'm not quite sure how to put the limits in, but they are from a to b.

I hope that helped!

 

[SammyS]

\displaystyle \int_{a}^{b}{\pi \left(f(x)\right)^2} dx

 

[None_of_the]

Hi,
Use two fonctions y=mx for a to b and y=k for b to c

add the result and multiply by two.

 

[SammyS]

As you rotate a cross section of the curve around the axis, it forms a cylinder, with radius y=f(x). and a thickness of δx.

The volume of that cylinder is given by:
A=\piy² δx

As the thickness of the cylinder approaches zero and you add (integrate) all the volumes of the reaaaaaly thin cylinders.
That gives the expression:

\int\pi\,f(x)²dx

I'm not quite sure how to put the limits in, but they are from a to b.

I hope that helped!

Actually, that should be,

The volume of that cylinder is given by:
A*δx = \piy² δx

 

[Endorser]

Thanks All, But how to we actually get from A=πy2 δx to ∫πf(x)2dx
How does the area become the volume?

 

[SammyS]

A is the area of a circle with radius y & y = f(x). That radius goes from the x-axis, vertically up to the graph y = f(x). Multiplying times δx (delta-x) gives the volume of a very thin circular disk of thickness δx . The integral from x=a to x=b indicates that the volume of a series of such disk is summed to give the total volume of the solid of revolution.

 

[mattg443]

The definition of an integral is adding (\sum) very skinny things (lim\delta x-->0) between two points.

If you are finding the area under a curve, you integrate between two points and are adding skinny rectangles (with almost no width i.e\deltax), which are practically adding lines. (you just add the heights \intydx)

With volumes, in this case, you are adding skinny cylinders, until the cylinder becomes practically a circle. (you just add the areas of those circles \int\piy²dx)

Adding lines gives an area
Adding areas gives a volume (just imagine adding all the areas of the pages of a book to get its volume)