How Do Ashcroft and Mermin Derive the Conversion from Equation 22.6 to 22.9?

[raisins]

Hi all,

I'm reading through Chapter 22 of Ashcroft and Mermin and am having difficulty deriving an equation. Could someone please show me (or outline the steps) how Ashcroft and Mermin convert the quadratic term in Eqn. (22.6) to Eqn. (22. 9)? (pictures attached).

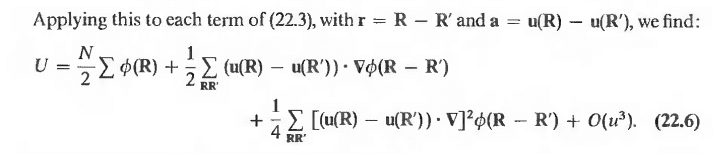
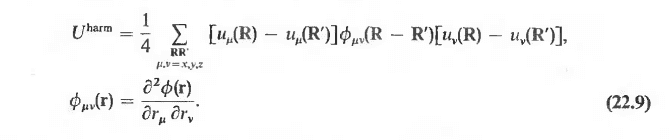
Thanks in advance :)

 

[dRic2]

That's just Einstein summation convention. If you imagine a vector-like quantity $\mathbf a = (a_1, a_2, ..., a_n)$, the dot-product with another vector-like quantity is the sum of the product of the i-components, that is $\sum_i a_ib_i$. With Einstein convention, you just don't write the $\sum_i$ and it is understood that a summation has to be performed for every repeated index like $a_ib_i$.

In this example the vector $\mathbf u(R) - \mathbf u(R') = \mathbf a$ and $\nabla = (\frac {\partial }{\partial x_1}, \frac {\partial }{\partial x_2}, ..., \frac {\partial }{\partial x_n}) = \mathbf b$. So, if you use the convention, you would write $[u_i(R) - u_i(R') ]\frac {\partial} {\partial x_i}$. Of course you have to do it 2 times because it is squared and that is way you get 2 indices and the second derivatives.

Note that if you look up Einstein convention for the dot product you might encounter expressions like $a_i b^i$. There is a reason to have "upper" and "lower" indices, but it is essential only when you are dealing with a non-cartesian system of coordinates (like in relativity). Here you are fine and don't need to bother.

 

[Haborix]

I concur with @dRic2's answer, but I think Ashcroft/Mermin are abusing notation. As far as I can tell, you have to assume that neither of the derivations act on the $u$'s of the other factor. If you tried to do the calculation in the normal course of index notation you might not get what they do.

 

[hutchphd]

The derivatives are partial derivatives. It means they operate only upon the indexed quantity. I do not see the problem.

 

[Haborix]

The derivatives are partial derivatives. It means they operate only upon the indexed quantity. I do not see the problem.

Ah, fair enough.