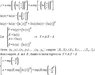How do I perform a weighted least squares fit with error bars?

[pergradus]

Hi, I am trying to do a best least-squares fit to a set of data which is described by the following equation:

y=a\exp(-b\ln^2(c/x))

Where a,b,c are constant parameters I am trying to find values for.

Any advice on how to proceed?

 

[JJacquelin]

You write ln(c/x)²
does it mean
(ln(c/x))² = (ln(x/c))²
or
ln((c/x)²) = -2 ln(x/c)
?

 

[pergradus]

You write ln(c/x)²
does it mean
(ln(c/x))² = (ln(x/c))²
or
ln((c/x)²) = -2 ln(x/c)
?

The former, I fixed it, sorry for the bad notation.

 

[JJacquelin]

You are lucky. After some transformations, it can be solved by linear regression (in attachment)

 

[pergradus]

You are lucky. After some transformations, it can be solved by linear regression (in attachment)

Thanks, I'm at home now, but in your attachment you're missing the 'b' parameter, does that change things?

 

[JJacquelin]

Damn ! I forgot the 'b' !
It doesn't change much : the simple linear regression becomes a multivariate linear regression.

 

[pergradus]

Damn ! I forgot the 'b' !
It doesn't change much : the simple linear regression becomes a multivariate linear regression.

Thanks! I was able to use that transform to produce a decent fit in MatLab - but I'm wondering, do I have to perform a transform on the error bars too if I want to weight the data?

 

[JJacquelin]

do I have to perform a transform on the error bars too if I want to weight the data?

Yes. Knowing the error ranges on the (x_i , y_i) it is possible to compute the error ranges on (X_i , Y_i , T_i).