dj-motion
- 2
- 0
hey, so I'm currently studying electronic engineering on year 2 of level 3 and having to study mechanical principles this year which I don't really know anything about and my tutor doesn't explain properly. I would appreciate some help on the method of calculating the questions. I've added clear images of the questions as there would be too much to type out
known equations that I need:
R=√(ΣFx^2+ΣFy^2)
θ=tan^-1(ΣFy/ΣFx)
σ=F/A
ε=σ/E
A=πr^2
τ=Fp/Ap
S=τ/Y
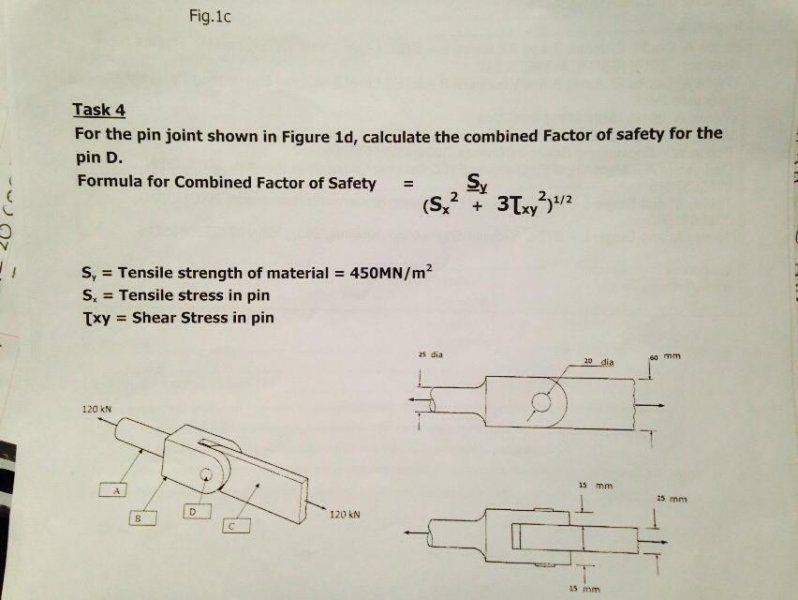
Combined Factor of Safety=Sy/(Sx^2 + 3τxy^2)^1/2
Attempt so far, not sure if it's correct but I've tried with limited knowledge about mech p.
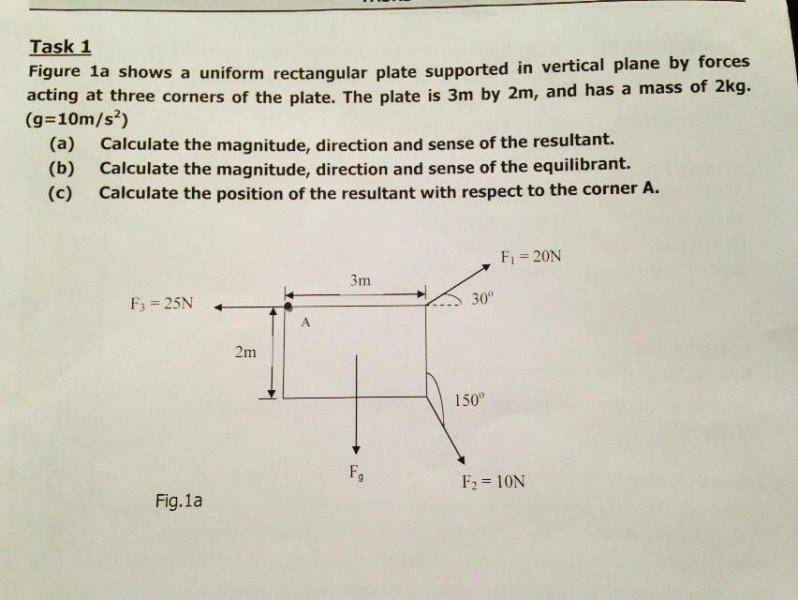
Task 1
a) Σfx=20cos(30) + 10cos(150) -25
=17.32-8.66-25
=-16.34N
Σfy=20sin(30) - 10sin(150) - (f=mg=2(10)=20N)
=10-5-20
= -25
R=√(16.34^2+25^2)
=√(267+625)
=√892
=29.87N
θ=tan^-1(-25/-16.34)
=56.83°
∴R=29.87N at an angle of 56.83° from the positive horizontal axis
b) Equilibrant=29.87N 180+56.83=236.83°
∴E=29.87N at an angle of 236.83° from the positive horizontal axis
C) I didn't really understand the question, I assumed it meant show the resultant on the space diagram but it says calculate so I'm not sure
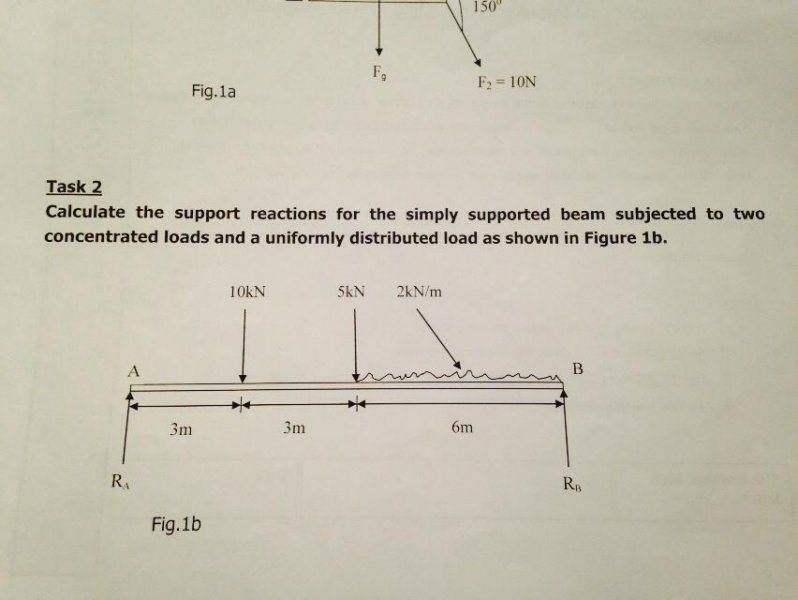
Task 2
Total load due to U.D.L=6x2=12KN
Centre load distance from Ra=6+3=9m
Centre load distance from Rb=3m
Taking moments of Rb:
Rb x 12 - 10 x 3 - 5 x (3+3) - (2x6)(9)
∴ 12Rb-30-30-108=0
∴Rb=(30+30+108)/12
=168/12
=14KN
Total load on beam = 10+5+(2x6) = 27KN
Ra+14=27
Ra=27-14
Ra=13KN
Task 3
a) A=πr^2=π30^2=900π=2827.43mm^2
σ=F/A=(30x10^3)N/(2.827x10^-3)m^2=10.61MPa
b) for strain I got 50.52x10^-6 using ε=σ/E
c) I got 0.126mm using dl=σlo/E
d) for shear stress I got 381.97MPa using τ=Fp/Ap
for shear strain I got 2.73 x 10^-3 using S=τ/y
Couldn't do Task 4 at all, I know there's a lot to read but would appreciate some help on abit of it lol cheers





known equations that I need:
R=√(ΣFx^2+ΣFy^2)
θ=tan^-1(ΣFy/ΣFx)
σ=F/A
ε=σ/E
A=πr^2
τ=Fp/Ap
S=τ/Y
Combined Factor of Safety=Sy/(Sx^2 + 3τxy^2)^1/2
Attempt so far, not sure if it's correct but I've tried with limited knowledge about mech p.
Task 1
a) Σfx=20cos(30) + 10cos(150) -25
=17.32-8.66-25
=-16.34N
Σfy=20sin(30) - 10sin(150) - (f=mg=2(10)=20N)
=10-5-20
= -25
R=√(16.34^2+25^2)
=√(267+625)
=√892
=29.87N
θ=tan^-1(-25/-16.34)
=56.83°
∴R=29.87N at an angle of 56.83° from the positive horizontal axis
b) Equilibrant=29.87N 180+56.83=236.83°
∴E=29.87N at an angle of 236.83° from the positive horizontal axis
C) I didn't really understand the question, I assumed it meant show the resultant on the space diagram but it says calculate so I'm not sure
Task 2
Total load due to U.D.L=6x2=12KN
Centre load distance from Ra=6+3=9m
Centre load distance from Rb=3m
Taking moments of Rb:
Rb x 12 - 10 x 3 - 5 x (3+3) - (2x6)(9)
∴ 12Rb-30-30-108=0
∴Rb=(30+30+108)/12
=168/12
=14KN
Total load on beam = 10+5+(2x6) = 27KN
Ra+14=27
Ra=27-14
Ra=13KN
Task 3
a) A=πr^2=π30^2=900π=2827.43mm^2
σ=F/A=(30x10^3)N/(2.827x10^-3)m^2=10.61MPa
b) for strain I got 50.52x10^-6 using ε=σ/E
c) I got 0.126mm using dl=σlo/E
d) for shear stress I got 381.97MPa using τ=Fp/Ap
for shear strain I got 2.73 x 10^-3 using S=τ/y
Couldn't do Task 4 at all, I know there's a lot to read but would appreciate some help on abit of it lol cheers