How to use Thevenin to find R and I?

[stipan_relix]

Homework Statement

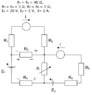
In the circuit shown, in the image, the variable resistor R is consuming maximum power. Determine:
a) resistance for R
b) power for R
c) current for R₃ and its direction

Homework Equations

The Attempt at a Solution

I tried getting I_A(the direction is shown with arrows in the picture under) like this: E₁-I_AR₃+IR₃-I_AR₄=0
-5I_A-5I_A=30-10
I_A=-2 A
but I have a feeling that's not good ^
---------------------------------------------------------------------------------------------------------------------------------

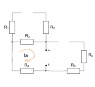
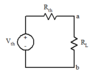
I calculated R_T using Thevenin: R_T=R_ab=R₃+R₄=10Ω
Then I got from the main scheme:
U_ab=-I_AR₄+E₁-I_AR₃+IR₃ = -(-2)*5+30-(-2)*5+10 = 60 V

I don't know how to proceed now.

 

[gneill]

Investigate the "Maximum power transfer theorem".

 

[stipan_relix]

Investigate the "Maximum power transfer theorem".

So according to the "maximum power transfer theorem", R=R_T=10Ω. Thank you.

From that, the equation for I_A should be:
E₁-I_AR₃+IR₃-I_AR-IR-I_AR₄=0
-20I_A=-30-10-20
I_A=3 A
and for U_ab:
Uab=-I_AR₄+E₁-I_AR₃+IR₃=40 V
Now I can get I_R=E_T/R_T+R=2 A and P_R=I²*R=2²*10=40 W. Hopefully I did everything right.

Although, now it asks me to get I_R3 and its direction, but isn't its direction already defined by the current source?

 

[stipan_relix]

Maybe it's: I_R3=I+I-I_A ? With direction to the left?

 

[gneill]

From that, the equation for I_A should be:
E₁-I_AR₃+IR₃-I_AR-IR-I_AR₄=0
-20I_A=-30-10-20
I_A=3 A
and for U_ab:
Uab=-I_AR₄+E₁-I_AR₃+IR₃=40 V
Now I can get I_R=E_T/R_T+R=2 A and P_R=I²*R=2²*10=40 W. Hopefully I did everything right.

Looks good. A simpler way would be to employ your Thevenin equivalent:

$I = \frac{V_{th}}{R_{th} + R_L}$

$V_{ab} = V_{th} \frac{R_L}{R_{th} + R_L}$

Although, now it asks me to get I_R3 and its direction, but isn't its direction already defined by the current source?

Not quite, since neither of the current sources is directly in series with $R_3$, and you may not be able to know off hand the effect of $E_1$ on the direction. However, you do now know all the currents but one entering/leaving the central node, so KCL at that node will settle the matter.

Maybe it's: I_R3=I+I-I_A ? With direction to the left?

Yup.

 

[stipan_relix]

Looks good. A simpler way would be to employ your Thevenin equivalent: V_ab=V_th*R_L/R_th+R_L

This gives me V_ab = 20V, but my way above got V_ab = 40V?

 

[gneill]

This gives me V_ab = 20V, but my way above got V_ab = 40V?

Oops, I missed that when I scanned your work. Although you shouldn't be getting 20 V either !

By the Thevenin method you know you've got a voltage divider with two equal resistances, hence the output should be 1/2 the source voltage, so one half $V_{th}$ or 30 V.

 

[stipan_relix]

Oops, I missed that when I scanned your work. Although you shouldn't be getting 20 V either !

By the Thevenin method you know you've got a voltage divider with two equal resistances, hence the output should be 1/2 the source voltage, so one half $V_{th}$ or 30 V.

I am confused now. Isn't the V_ab I got also V_th? Where did you get 30 V from?

 

[gneill]

I am confused now. Isn't the V_ab I got also V_th? Where did you get 30 V from?

See the diagram in post #5.

You calculated $V_{th} = 60\;V$ and $R_{th} = 10\;\Omega$. Half of $V_{th}$ is $30\;V$.

 

[stipan_relix]

See the diagram in post #5.

You calculated $V_{th} = 60\;V$ and $R_{th} = 10\;\Omega$. Half of $V_{th}$ is $30\;V$.

It says 40V for me, not 60V?

I also thought V_ab = V_th?

 

[gneill]

In your very first post you correctly calculated the open circuit voltage $U_{ab}$ which is the Thevenin voltage. Once you attach a load across the output, it will no longer read $V_{th}$ but some fraction of it depending on the size of the load resistance and $R_{th}$.

 

[stipan_relix]

In your very first post you correctly calculated the open circuit voltage $U_{ab}$ which is the Thevenin voltage. Once you attach a load across the output, it will no longer read $V_{th}$ but some fraction of it depending on the size of the load resistance and $R_{th}$.

Alright, but how does that fit into the maximum power transfer theorem if R_T=R=10Ω then gives me I_A=3 A and with that I_A I get V_ab=40V?
Because the first time I solved for I_A, I did it like R wasn't there at all, but since R_T=R=10Ω, shouldn't I solve it using R in the equation as well?

 

[gneill]

Alright, but how does that fit into the maximum power transfer theorem if R_T=R=10Ω then gives me I_A=3 A and with that I_A I get V_ab=40V?
Because the first time I solved for I_A, I did it like R wasn't there at all, but since R_T=R=10Ω, shouldn't I solve it using R in the equation as well?

Yes. For the Thevenin version you've two resistors forming a voltage divider. Each of them is 10 Ω. Also,

3 A * 10 Ω = 30 V.

 

[stipan_relix]

Okay I think I kind of understand it now. Thank you.