How Do You Calculate Elevator Cable Forces for Maximum and Minimum Motor Load?

[lmf22]

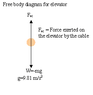
An elevator (mass 4100 kg) is to be designed so that the maximum acceleration is 0.0700g.
What is the maximum force the motor should exert on the supporting cable?
What is the minimum force the motor should exert on the supporting cable?

I converted the acceleration to .6867 m/s^2 and plugged that and the mass into F=ma, but the answers doesn't seem to be right.

 

[Leong]

Upward direction positive; downward direction negative
\begin{array}{cc}<br /> Newton&#039;s\ 2nd\ Law\\<br /> \sum \vec{F}=m\vec{a}\\<br /> F_{ec} + W =ma \ with \ a= \ The \ elevator&#039;s\ acceleration\\<br /> F_{ec} + (-mg) = ma\\ <br /> F_{ec} = m(a+g)\\<br /> F_{ec_max}= m(0.0700g+g)\ When\ a=+0.0700g\ ie\ The\ elevator \ accelerates\ upward\\<br /> F_{ec_min}= m(-0.0700g+g)\ When\ a=-0.0700g\ ie\ The\ elevator \ accelerates\ downward\\<br /> \end{array}

 

[M98Ranger]

The maximum force that the motor should exert on the supporting cable would be equal to the weight of the elevator plus the force needed to accelerate it. The weight of the elevator can be calculated using the formula Fg = mg, where m is the mass of the elevator and g is the acceleration due to gravity (9.8 m/s^2). So, Fg = (4100 kg)(9.8 m/s^2) = 40180 N.

To find the force needed to accelerate the elevator, we can use the formula F = ma, where m is the mass of the elevator and a is the acceleration (0.6867 m/s^2). So, F = (4100 kg)(0.6867 m/s^2) = 2815.47 N.

Therefore, the maximum force the motor should exert on the supporting cable would be 40180 N + 2815.47 N = 42995.47 N or approximately 43 kN.

The minimum force that the motor should exert on the supporting cable would be equal to the weight of the elevator minus the force needed to decelerate it. So, the minimum force would be 40180 N - 2815.47 N = 37364.53 N or approximately 37 kN.

It is important to note that these calculations assume ideal conditions and do not take into account factors such as friction and air resistance, which may affect the actual forces needed to accelerate and decelerate the elevator.