How Do You Calculate Net Torque Without Knowing the Center of Mass?

AI Thread Summary
To calculate net torque without knowing the center of mass, one can analyze the system as a couple, where two equal and opposite forces create rotational effects. The net torque can be determined by calculating the torque about different reference points, which can provide insights into the system's behavior. The forces applied are 59.0 N each, acting at an angle of 37.0° on a 13.6 cm long object. Understanding the torque generated by these forces does not strictly require the center of mass, as the couple's effects can be evaluated from any point. Ultimately, the key is to apply the principles of torque calculation effectively, regardless of the center of mass location.
shashusad
Messages
4
Reaction score
0
In the following question, I'm unable to find the center of mass to do the Torque calculation:

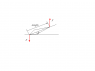
Two 59.0 N forces are applied in opposite directions to the 13.6 cm long figure shown. If the angle θ=37.0°, what is the net torque about the center of mass?

Image: http://www.freeimagehosting.net/image.php?02a6935f86.png
 

Attachments

  • kn-pic1312.png
    kn-pic1312.png
    1.2 KB · Views: 785
Physics news on Phys.org
Hint: These forces form a couple.
 
I get that the forces form a couple. I could do the Torque calculation but I can't figure out the center of mass of the object
 
shashusad said:
I get that the forces form a couple. I could do the Torque calculation but I can't figure out the center of mass of the object
Does it matter? Hint: Try finding the torque about two different points.
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Calculate the speed and angle of the center of mass before a collision
Replies
3
Views
851
Angular momentum conservation on a merry-go-round
Replies
5
Views
2K
Torque and Angular Momentum - Origin Misconception
Replies
5
Views
2K
Distribution of Energy when work is done on a system of 2 masses connected by a spring
Replies
17
Views
1K
Where is my mistake? (Pure rolling and center of mass)
Replies
8
Views
2K
Help Me Solve My Diagram Problem: Calculating Center of Mass
Replies
8
Views
2K
Question about springs and rotational/translational energy
Replies
4
Views
1K
Solving Force by Table Leg: Find F_A & F_B
Replies
2
Views
3K
Net Torque of 2 Forces: Calculate for 59.9N, 28.3cm, 29.6°
Replies
10
Views
5K
Rolling Bottle: Calculating Acceleration of Center of Mass
Replies
2
Views
1K

Hot Threads

Recent Insights

Back
Top