How Do You Calculate the Motion of a Pebble in a Rolling Tire?

[HeLLz aNgeL]

Homework Statement

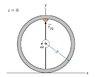
You are to find the coordinates of a pebble stuck in the tread of a rolling tire that is rotating counterclockwise (i.e., in the positive sense) with angular velocity omega. The tire rolls without slipping on the ground (which is at y = 0 ). The outer radius of the tire is R. At time t = 0 , the pebble is at the top of the tire, as shown.

a). Find the velocity of the axle of the tire relative to a fixed point on the ground, v_vec_ag(t). Note the order of the subscripts: velocity of axle measured relative to the ground. Express your answer in terms of R, omega, and x_unit and/or y_unit.

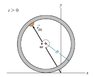
The pebble and tire have now rolled as shown in the figure. View Figure Answer the following questions for t>0.

b). Find the position vector of the pebble relative to the initial point of contact between the wheel and ground at a time t, r_pg_vec(t).
Express the position vector of the pebble in terms of R, omega, t, and the unit vectors x_unit and/or y_unit of the xy coordinate system shown.


c). Find v_vec_pg(t), the velocity vector of the pebble with respect to a fixed point on the ground, in terms of the unit vectors x_unit and y_unit of the xy coordinate system shown.
Express the velocity vector in terms of R, omega, t, and x_unit and/or y_unit.


d) Now find a_vec_pg(t), the acceleration vector of the pebble with respect to a fixed point on the ground.
Express your answer in terms of R, omega, t and x_unit and/or y_unit of the xy coordinate system shown.

The Attempt at a Solution

ok, for the first one, i know v = rw, but how do i write it in terms of vectors, v =rwx ?

and for part b, i have no clue how i should be approaching this ... just seems too weird :S

 

[learningphysics]

I think for part a), what they want is:

v_vec_ag(t) = -Rw\hat{x}... ie -Rw times a unit vector in the x-direction.

For part b), suppose the wheel was just rotating without any translation... (ie it is just rotating in place). What is the position vector relative to the initial point of contact? use sin, cos etc... the angle through which the wheel has rotated is wt...

then how does this position vector change when you take into account the horizontal velocity of the tire?

c) take the derivative of b).

d) take the derivative of c).

 

[HeLLz aNgeL]

ok, so i know its Rsinwt(x) + RCoswt(y) and the initial position was just R(y)

so, relative to the initial position it should be Rsinwt(x)+(R(y)-RCoswt(y))

doesnt sound right, does it ?

 

[HeLLz aNgeL]

bump ... anyone ?

 

[learningphysics]

ok, so i know its Rsinwt(x) + RCoswt(y) and the initial position was just R(y)

so, relative to the initial position it should be Rsinwt(x)+(R(y)-RCoswt(y))

doesnt sound right, does it ?

Well... if translation wasn't there... here's what I get:

\vec{r} = -Rsin(wt)\hat{x} + (Rcos(wt)+R)\hat{y}

Now add the translation... -Rwt\hat{x}

so it comes out to:

\vec{r} = (-Rsin(wt)-Rwt)\hat{x} + (Rcos(wt)+R)\hat{y}